SE20101110034

, >;Działante neuronu polega na odebraniu informacji poprzez dendryt i pfp tworzeniu odebranego sygnału zgodnie z ustaloną regułą. Jeżeli sumaryczny sygnał wejściowy przekroczy pęy^ięh ustalony próg, to neuron zostaje pobud*n ny i za pośrednictwem aksonu sygnał przekazywany jest do innych komórek (neuronów), które działają w analogiczny sposób.

Jedną z najważniejszych cech neuronu jest to, że modyfikuje on swOjr działanie wykorzystując informacje otrzymywane z zewnątrz. Taki proce* zmian nazywany jest uczeniem. Bardzo ważną rolę w tym procesie odgrywki synapsy, a w zasadzie wagi synaptyczne, które ulegają zmianom (właśni® Ir wagi decydują o poziomie pobudzenia neuronu). Kolejne neurony, popfiMM dendryty, łączą się ze sobą za pomocą synaps, tworząc sieć neuronów, DIm przykładu, mózg ludzki składa się z około 100 miliardów neuronów. Liczba połączeń między komórkami wynosi około 10 tysięcy bilionów. SzybkOlf pracy mózgu szacuje się na około 10 trylionów operacji na sekundę, co w porównaniu z najszybszymi komputerami (do 100 miliardów operacji na sekuił dę) jest wręcz niewyobrażalne.

Model neuronu i sieci neuronów

Biologiczny neuron jest modelowany¹ (rysunek Z.2.2) w celu uzyskaniu podstawowego elementu (“cegiełki”) do budowy większych modeli (cał®gu mózgu czy jego części) sieci neuronowych. Pojedyncze neurony łączon® I® w warstwy (rysunek Z.2.3).

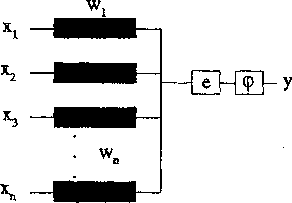
Ryś. Z.2.2. Model pojedynczego neuronu cp(e) — funkcja aktywacji neuronu; y ~ (p{e) — wartość sygnału wyjściowego; e ■— Xi Wf— sumaryczne pobudzenie neuronu

Wektor wyjściowy Y wyznacza Si® U® podstawie poniższej zależności²:

Y=ę(W^TX)    (Z.2,1)

gdzie: W—macierz wartości wag ncuiu nów sieci,

X — wektor sygnałów wejściu wych.

Dla pojedynczego m-tego neuronu WM tość sygnału wyjściowego wynosi:

y„ = <p(W"X)    (Z.U)

gdzie: W^m — m-ta kolumna (transponowa-na) macierzy W zawierająca wartości wag m-tegó neuronu.

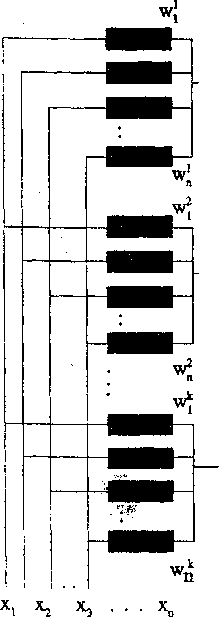
neuron 2

neuron k

Rys, Z.2,3. Model warstwy neuronów

Z kolei warstwy neuronów łączone są ze sobą, tworząc tzw. sieci neuronowe wielo-~ -Y\ warstwowe (rysunek Z.2.4).

Wartość wektora wyj ścio wego Y sieci dla neuron 1 liniowych neuronów (neuronów o liniowej funkcji aktywacji) wyznacza się następująco:

(Z.2.3)

Y = W? Wl_t... W₂^r W?X

a dla nieliniowej funkcji aktywacji:

K=<p(Wf(p<W^_₁... (p(Wl(p(WlX))))(Z2.4)

gdzie: Wj^r—jest transponowaną macierzą wartości wag i-tej warstwy sieci.

W powyższym wzorze widać kierunek³ przepływu sygnałów od wejścia (reprezentowanego przez macierz Wj) do warstwy wyjściowej opisywanej przez macierz W_k.

Uczenie neuronów i sieci neuronowych Podstawowym problemem związanym z sieciami neuronowymi jest zagadnienie uczenia sieci neuronowych. Na potrzeby uczenia sieci neuronów zdefiniowano tak zwany ciąg uczący. Stanowią go pary wektorów:

U = {<X_x ,Z_X> ,<X₂,Z₂> ,,<X_N,Z_N>)    (Z.2.5)

gdzie: N — długość ciągu uczącego (liczba wzorców);

<X₍, Zz> — para ucząca;

X_t =    , 4 ,..., x^lr) — wektor opisujący i-ty wzorzec;.

n — liczba wejść sieci;

67

1

   Programowo lub sprzętowo.

2

   Często jako funkcję aktywacji przyjmuje się funkcję, logistyczną o postaci: cp(e) = 1/(1 +exp( (U)}, gdzie P jest współczynnikiem określającym kształt funkcji.

3

Istnieją struktury sieci zawierające sprzężenia zwrotne, w których sygnały mogą przebiegać w obu kierunkach. Założenie, że w sieci wielowarstwowej sygnały przebiegają w jednym kierunku umożliwia wyznaczenie błędu 5; dla poszczególnych warstw.