skanowanie0071

a = g

m₂sin/?—n^sina m₁+m₂

m/s²

Zadanie 6.15. Wózek jadący na czterech kołach może poruszać się po poziomym torze. Masa wózka bez kół wynosi m_{ kg, masa każdego, z kół m₂ kg, a promień r m. Koła należy traktować jako pełne, jednorodne walce. Do wózka przyczepiono nieważką i nierozciągliwą nitkę, przerzuconą'przez krążek o masie m₃ kg i promieniu R m. Na drugim jej końcu przywiązano obciążnik o masie m₄ kg (rys. 6.33). Obliczyć, po jakim czasie wózek przejedzie drogę/ m Jeżeli w chwili początkowej wózek był nieruchomy. Należy przyjąć, że nie ma poślizgu między kołami wózka a torem i między nitką a krążkiem.

Odpowiedź

£ m

2(m₁ + m_Ą + 4 m₂)+ m-s 2gm₄

s

Zadanie 6.16. Ciężarek A o masie m₁ kg połączono linką przez nieważki krążek z ruchomym jednorodnym walcem o masie m₂ kg i promieniu R m. Drugi koniec liny zamocowano w punkcie B (rys. 6.34). Linka jest nieważka i nieroz-ciągliwa. Obliczyć przyspieszenie ciężarka A.

Odpowiedź

2m, — m₂    ,

A-g—I- m/s

2m_ł

Zadanie 6.17. Na poziomej płaszczyźnie ułożono dwa doskonale chropowate Jednorodne pełne walce o masach m₁ kg i promieniach r m tak, że osie walców pozostają równoległe (rys. 6.35). Na walcach ułożono deskę'o masie m₂ kg połączoną nierozciągliwą i nieważką nicią, przerzuconą przez nieważki krążek,¹

Rys. 6.34. Do zadania 6.16

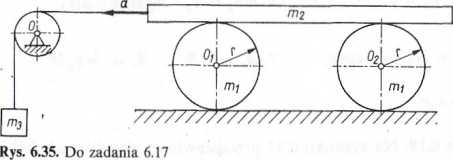
się w potu przyciągania ziemskiego.

Odpowiedź

8m₃    , 2

a = o—-^—-— m/s

8(m₂+m₃)+3m₁

Zadanie 6.18. Na rysunku 6.36 przedstawiono układ trzech kół i ciężar A o masie m kg. Koło ruchome o masie m i promieniu R m toczy się bez poślizgu po poziomym torze i jest napędzane stałym momentem M N • m. Współczynnik tarcia tocznego koła po torze wynosi f Ciężar A leży na chropowatej równi pochyłej o kącie pochylenia a, a współczynnik tarcia ślizgowego wynosi ju. Dwie liny, do których przymocowano koło i ciężar, są nawinięte na dwa współśrod-kowe kofa zamocowane przegubowo w punkcie 0. Masy tych kół są równe m i 2m, a ich promienie wynoszą r i 2r. W chwili początkowej układ znajdował się w spoczynku. Napisać równania ruchu i równania więzów.

Odpowiedź

1. ma_t= —T—S_lt 2. m O — N—mg, 3. ^m^- e_t = M+ TR — Nf