skanuj0034 (5)

214    V/. Funkcjo w»H/ rmionnych

Podaną w definicji warstwicy równość /(x) = c nazywamy równaniem war-stwicy (izokwanty).

Warstwica jest więc zbiorem tych punktów x z dziedziny D_f funkcji f, dla których /(x) = c. Warstwicę l_f(c) można też interpretować jako rzut na dziedzinę D_f przekroju wykresu W_f płaszczyzną z = c (prostopadłą do osi Oz w punkcie c). Ilustrację tej interpretacji dla pewnej funkcji dwu zmiennych przedstawia rys. VI. 1.8.

Uwaga: Warstwica IAO) jest zbiorem miejsc zerowych funkcji wielu zmiennych /.

Dla pewnych c warstwica I_f(ć) może być zbiorem pustym i dzieje się tak wte-dy, gdy c nie jest wartością funkcji (c ff /(£Jy)).

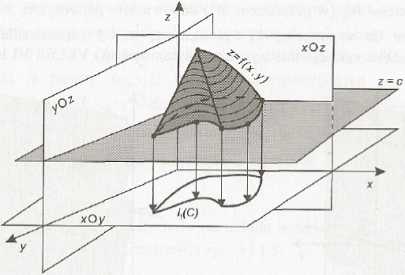
Rys. VI.1.8

Przykład VI.1.7

Podamy równania warstwie i narysujemy je dla funkcji / i g omówiony* w przykładzie VI. 1.5, których wykresy przedstawiają rysunki VI. 1.3 i VI. 1.4.

Dla funkcji f[x_l,x₂) = 4 - 2x_y + x₂ warstwicą odpowiadającą wartości c jea zbiór: l_f{ć) = {(x_vx₂) e IR²: 4 - 2x_L +x₂ = cj. Każda jej warstwica jest więc prostą o równaniu x₂ = 2x_] + c - 4. W układzie współrzędnych 0x_tx₂ tworzą oj rodzinę prostych równoległych. Na rys. VI. 1.9 zaznaczono warstwicę odpowiadające: c = -1,, c - 2, c = 4, c, = 8. Są to więc proste o równaniach:

x₂ = 2x_y +4.

x₂ = 2x_t -5, x₂ = 2x_{ -2, x₂ = 2Xj,