TOB18

W celu obliczenia funkcji macierzy _e^At wykorzystujemy metodę Cayleya--Hamiltona

e^At = Oo(t)l + «i(t)A Aby obliczyć ao(t) oraz Ui(t), stosujemy równanie

	e^i	~ ®o(t) + oti(t)Ai
	de^A*‘	d	r ~\
	dA2	■14 II	0Co(t) + «l(t) K
czyli
	e^	‘ = ao(t) + «i(t)^i
		te^' = ao(t)
a więc
	e	' = Oo(t) - «l(t)
		te^-	' = OCi(t)
stąd
		aŁ(t) = te '
	ao(0 =	te^-' + e^-' = e^-'(t + 1)
Funkcja macierzy			r 1

_aAt

(te ‘ + e

+ te-

i::]

2    ¹

1 _3 L 4    2 J

x_p = e^A'x_p(0)

W celu wyznaczenia macierzy x_p(0) obliczamy

x,_P(0) = _Mq(0) = u_c(0) - u_Cu = 40 - 50 = -10 V *2,(°) = i_Ł,(0) = i_Ł(0) - i_Lu = 20 - 25 = -5 A

Zatem

Ostatecznie

*,(»)=[ _^ł®]

₌ f["te-^t + e-^t 0 I J” — 0,5te^-*    —te"*    10“l

[L ⁰ te^-'+ e^-‘J ⁺ |_ 0,25te^-'    —l,5te^_tJj[_ —5J

_T- 10e^-r

~L -⁵H «_Cp(t)*x_lp = - 10e"‘V

k_P{t) = x_2p = — 5e^-'A

Uwzględniając obliczone uprzednio składowe ustalone, otrzymamy «c(0 = «cu + «cp = (50 - 10e~‘) V

k(t) = ku + k_P = (25 - 5 e ‘)A

5.5. Zadania do samodzielnego rozwiązania

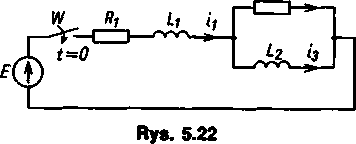
5.22. Obwód przedstawiony na rys. 5.22 znajduje się w stanie zerowym. Obliczyć prądy w stanie nieustalonym powstałym po zamknięciu łącznika W w chwili t = 0. Dane: E = 96 V; = 160 fi; 1?₂ = 90 Q; L_x = 0,1 H; L₂ = 0,036 H.

^r2 ii

Odpowiedź

i₂ = (0,6 - 0,8 e^-1000' + O,2e^-4000t) A i₃ = O,32(e~^1000t — e^-4000t) A h ⁼ h + *3

5.23. W obwodzie jak na rys. 5.23 w chwili t = 0 nastąpiło otwarcie łącznika W. Obliczyć napięcie na zaciskach otwartego łącznika w stanie nieustalonym dla dwóch przypadków:

a)    wymuszenia napięciowego £,

b)    wymuszenia prądowego I.

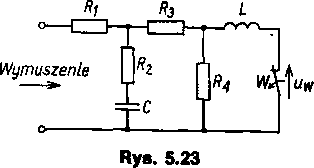
Dane: E = 10 V — napięcie stałe; / = 10 A — prąd stały; R_t = R₂ = Rj = = R₄ = 10Q; C = 10mF; L = 0,1 H.