FizykaII37101

3(?7

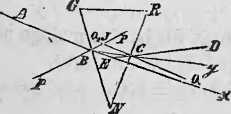
Fig. 206.

- cj --------«

łożywszy kąt padania na ścianę GN pryzmy, t. j. ABP = «, odpowiedni kąt załamania P'BC=fi, kąt padania na tylną jćj ścianę RN, t. j. BCQ= y, a kąt załamania Q'CD = S, tudzież kąt odchylenia DEx = D, nareszcie kąt łamiący pryzmy GNR a współczynnik załamania przy wejściu promieni ^z powietrza do pryzmy = n, mamy

t. j. Iajt odchylenia czyli dewiacji promieni, występujących z pryzmy w kierunku CD, od kierunku ich Ax przy wejściu do nićj, ma wartość najmniejszą. Dla uzasadnienia tego ostatniego wniosku, po-

DEx =EBCĄ-BCE, a dla EBC= P'BE — P'BC= ABP — P’BC — a — fi, i BCE —    — BCQ = <2'CZ> —    -—8—y, także

• Dfe = D = a — /3-f-ó — 7 = « -f-5 — (fiĄ-y)-Atoli    p>JC = JBCĄ-BCJ = P'BC + BCQ — fi Ą-y,

a oraz P'JC= GNR = ty, gdyż w czworoboku BJCN kąty Przy B i C są proste, zatćm BJC Ar ty — 180° = BACĄ- P'JC, tudzież    1) tp — fiĄ-y, a nareszcie

2)    D = a Ą- S — ty.

Gdy zaś sin a : sin fi = n : 1, sin y : sin 6 = l:n, więc także

3)    sin a — n sin fi,

4)    sin 8 — n sin y.

Cztery te zrównania orzekają związek, jaki między kątami ^fti fi,y, 8 i D zachodzi. Rozważmy teraz, jaki wpływ bardzo biała zmiana kąta padania « wywiera na resztę kątów. Dajmy ba to, że a rośnie; wówczas także (A powiększać się musi, a y ⁰ tyleż pomniejszać, gdyż suma fi Ą-y— ty j^est ilością stałą, ^zatćm kąt 8 również mniejszym stać się musi. Jeśli tedy kąt Padania a rośnie o małą ilość fi zaś. o fi', która to ilość równoczesny ubytek kąta y wskazuje, a 8' jest odpowiedni uby-tek kąta załamania 8, nareszcie /Ą zmiana kąta odchylenia D, którą ze znaczkiem -f- jako narostek, ze znaczkiem zaś — jako bkytek uważać należy,, będziemy mieli

DĄ-    n Ą- a'Ą- 8 — 8' — ty,

^a po wypuszczeniu równych ilości na obu stronach

A = o' — 8‘-