0307

309

§ 6. Iloczyny nieskończone

Zastąpmy teraz każdy z czynników 1 czynnikiem (1T ——) e^±x"^m- Łatwo widać, że nie wpły-

W7t    \ tffi /

nie to ani na zbieżność iloczynu, ani na jego wartość. Tymczasem nowy iloczyn nieskończony jest już bezwzględnie zbieżny, bo [125, 1])

i czynniki poczynając od pewnego miejsca są dodatnie i mniejsze od jedności.

5) Udowodnić tożsamość (dla 0<4<1)

(l+9)(l+₉^J)(l+9³)

(Euler).

Wskazówka. Zbieżność obydwu iloczynów stwierdzamy za pomocą 5°. Przedstawić pierwszy z iloczynów w postaci

(1-₉)(1-9^J)(1-9^S)...

6) Udowodnić, że dla <x>j8

Mm W+*)-(*+"— 1) - o.

■-co *(* + 1) ... (at + if-1)

W tym celu wystarczy wykazać rozbieżność iloczynu nieskończonego

a-0    a-O

lub szeregu [patrz 7°]

00

Y*=L,

Z_j tx+n

R«1

a to łatwo wynika z porównania z szeregiem harmonicznym.

Uwaga. Przykład ten, podobnie jak następne, jest poucząjący dlatego, że pokazuje, jak czasami naprawdę wygodnie jest sprowadzić poszukiwanie granicy ciągu do badania iloczynu nieskończonego z wykorzystaniem całej rozwiniętej teorii iloczynów nieskończonych.

“o f

7) Wróćmy do szeregu ^ ^    - , który rozpatrywaliśmy już w ustępach 370, 2) (e) i 378, 1) (e).

Pozostawiliśmy tam otwarte zagadnienie, jak zachowuje się szereg na końcu x = — 1 je przedziału zbieżności.

W tym przypadku otrzymujemy szereg

CO

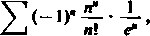
a-l

którego wyrazy zmieniają kolejno znak i maleją monofonicznie co do bezwzględnej wartości. Gdy przypomnimy sobie twierdzenie Leibniza [381], widzimy, że zbieżność tego szeregu zależy od tego, czy zachodzi równość

lim-

= 0.

n-»oo e"