0343

345

§ 9. Sumowanie szeregów rozbieżnych

419. Twierdzenie Taubera. Jeżeli szereg (A) jest sumowalny do A metodą Poissona-Abela, to jak widzieliśmy, może on nie mieć sumy w zwykłym sensie. Innymi słowy, z istnienia granicy

00

(5)    lim V a, z* = A

*-1-0 —o

nie wynika na ogół zbieżność szeregu (A). Powstaje naturalne pytanie, jakie dodatkowe warunki trzeba nałożyć na wyrazy tego szeregu, aby z (S) można było wnioskować, że szereg (A) jest zbieżny, tzn. że istnieje jego suma A w zwykłym sensie.

Pierwsze twierdzenie w tym kierunku udowodnił A. Tauber; głosi ono:

Niech szereg (1) będzie zbieżny dla 0<x< 11 niech zachodzi równoit (5). Jeżeli wyrazy szeregu (A) są takie, że

(6)    lim ^g|+2a*⁺ +^na" _ O,

•-•OO    W

to

£a. = A.

»-o

Dowód rozbijemy na dwie części. Najpierw założymy, że

lim na, = O, czyli

(*)•

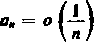
Jeżeli oznaczymy

6. = max Ikoil,

to przy n-r oo ó, będzie dążyło do zera monofonicznie malejąc.

Dla dowolnego naturalnego N mamy

a,-A =    o„(l -jt*)- £ °-**+ g. x‘-A\ ,

*-0    gaO    ft-W+I    H-0

wobec czego

i«0    r-0    it-N + 1    ^    i"0

(N+Dd-jc)

Weźmy dowolnie małą liczbę e>0 i przyjmijmy

(1 — x) N = e, czyli x — 1--~,

N

(') Stąd wynika już na mocy znanego twierdzenia Cauchy’ego [33, 13)], że spełniony jest warunek (6), ale nie na odwrót, wobec tego wychodzimy teraz od szczególniejszego założenia niż (6).

(’) Korzystamy przy tym z oczywistych dla 0<jt<l nierówności

l-*" = (l-x)(l+x+x²+ ... +x"-‘) < « (1 —x)

oraz

s *■

»-/*+!

v» + ^l

= -— < \-x

1

\-x '