0389

391

§ 3. Zastosowania

o sumie <p{k) i pomnóżmy oba szeregi przez siebie według reguły Cauchy’ego. Łatwo można napisać kilka pierwszych wyrazów tego iloczynu.

= l+(m+k)x+    >> _+mic₊ iiŁliiJ **+ ... ₌

= l+(m+k)x+ S^m+k)(^m+.^krH _x*+ ...

1-2

Współczynnikiem przy x?/n\ będzie oczywiście pewien wielomian całkowity n-tego stopnia względem m i k. Jaką będzie on miał postać? Jeśli m i k są dowolnymi liczbami naturalnymi większymi od n, to z elementarnych rozważań wynika, że współczynnik ten będzie miał postać

(m+k) (m+k—l) ... (m+k—n+1) .

A więc (jak to wynika z algebraicznego twierdzenia o równości wielomianów dwóch zmiennych) tę samą postać będzie on miał dla dowolnych m i k. Tak więc szukana funkcja q> (m) spełnia równanie funkcyjne

tf (m)-q> (*) = <f {m+k).

Stwierdzimy teraz ciągłość funkcji <p (m). Wynika ona ze zbieżności jednostajnej szeregu dwumien-nego dla wszystkich wartości m nie większych co do wartości bezwzględnej od dowolnie obranej liczby m_o>0. Dla tych wartości majorantą jego będzie szereg zbieżny

i+«„!*!+ -y°(.SŁ+JI |jr|²-f    °-+²> _w»+...

Z tego, jak wiemy [75,1°], wynika

q> (ni) = o" .

Ponieważ a = <p (l) = \ + x, więc ostatecznie

<p (m) = (1+jc)" •

5) Znany już czytelnikowi szereg logarytmiczny [405, (17)] można otrzymać z szeregu dwumiennego [407, (22)] za pomocą zależności [77,5 (b)]

In a = lim k (i/iT— l) (* = 1,2,3,...).

Przyjmijmy a = 1 +x (gdzie |jc(< 1) i podstawmy za (i +x)^u* rozwinięcie

(!+*)■'*= 1+-U+

k

.. +

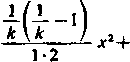
1-2-

*"+

Wtedy ln (1 +x) otrzymamy jako granicę wyrażenia

(2,    * „i +,)'»- .1 - «- -f- (.- }) + f (i -(, -    - ...

...    (,-L) ...    ...

dla k -*■ oo .

Wyrazy tego szeregu (dla stałego *) zawierają jako zmienną parametr naturalny k. W całym obszarze zmienności szereg (2) jest zbieżny jednostajnie względem k. Wynika to (przy zastosowaniu kryterium Weierstrassa) z tego, że jego majorantą jest szereg

W+ -!*£- +    + ... +    + ... (x = const, U! < 1)

2    3    n