1057

wania kolejnych krzywych stożkowych przyjęto pionowy stożek obrotowy, którego wszystkie tworzące mają z płaszczyzną podstawy kąt a.

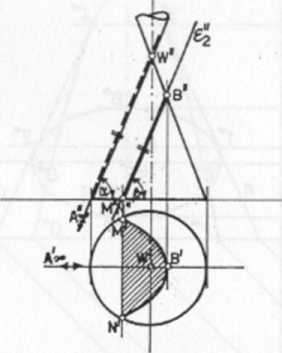
Rys. 110. Przekrój płaszczyzną gdy Za = Z/3 jest parabolą. Gdy płaszczyzna tnąca e₂ przechodzi przez wierzchołek, parabola zdegeneruje się do prostej

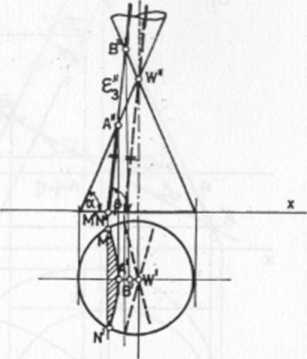
Rys. 112. Przekrój płaszczyzną £j, gdy Za < Z/3 jest hiperbolą. Gdy płaszczyzna przechodzi przez wierzchołek, hiperbola zdegeneruje się do dwóch prostych

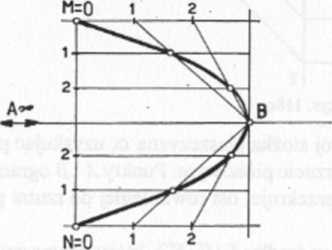
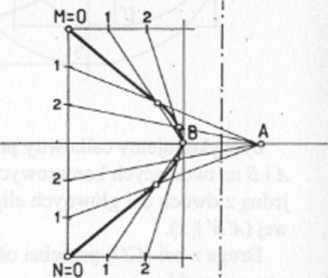
Rys. 111. Z osi paraboli BA i dwóch punktów MN należących do odcinka przekroju podstawy stożka płaszczyzną £_y budujemy równoległobok i dzielimy na pewną liczbę równych części pół odcinka MM oraz pół boku równoległoboku. Następnie łączymy punkt B z 1 \Az\_tBz2\Az2 itd. Punkty otrzymane z przecięcia odpowiednich prostych pozwalają wykreślić parabolę

t

Rys. 113. Z osi hiperboli AB oraz dwóch punktów MN, należących do odcinka przekroju podstawy stożka płaszczyzną e_y budujemy równoległobok i dzielimy na pewną liczbę równych części pół odcinka MN oraz pół boku równoległoboku. Następnie łączymy odpowiednio punkty A z 1 i Bzl, A z 2 i B z 2 itd. Punkty otrzymane z przecięcia prostych pozwalają wykreślić hiperbolę

7.3. Stożek - przekroje, przenikania, rozwinięcia 7.3.1. Punkt przebicia prostą a powierzchni stożka

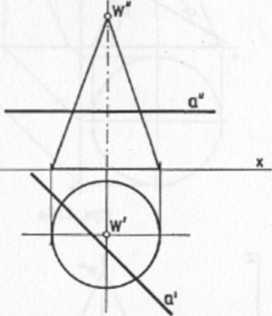
Rys. 114. Ustalić punkty przebicia prostą poziomą a powierzchni stożka obrotowego

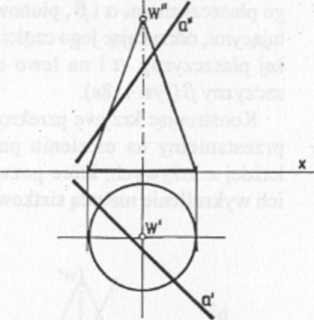
Rys. 116. Ustalić punkty przebicia dowolną prostą a powierzchni stożka obrotowego

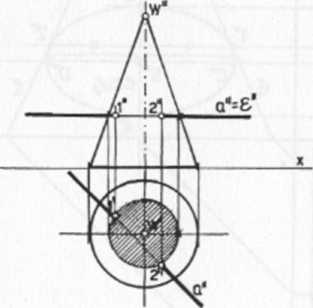
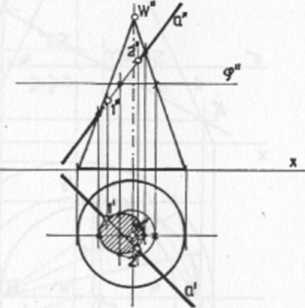
Rys. 115. Rozwiązanie uzyskano przez przeprowadzenie przez prostą płaszczyzny rzutującej £ równoległej do podstawy, tnącej powierzchnię stożka w okręgu. Tam, gdzie rzut poziomy prostej przecina okrąg przekroju płaszczyzną £ znajdują się rzuty poziome punktów, w których prosta przebije powierzchnię stożka

Rys. 117. Rozwiązanie uzyskano przez poprowadzenie przez prostą a płaszczyzny £. W przykładzie zastosowano płaszczyznę pionowo rzutująca, która przecina stożek w elipsie. Na przecięciu rzutu poziomego prostej i elipsy znajdują się rzuty poziome szukanych punktów przebicia

115