1140

Praktyczne wykorzystanie powyższych formuł prezentują przykłady 8.1 i 8.2.

Przykład 8.1.

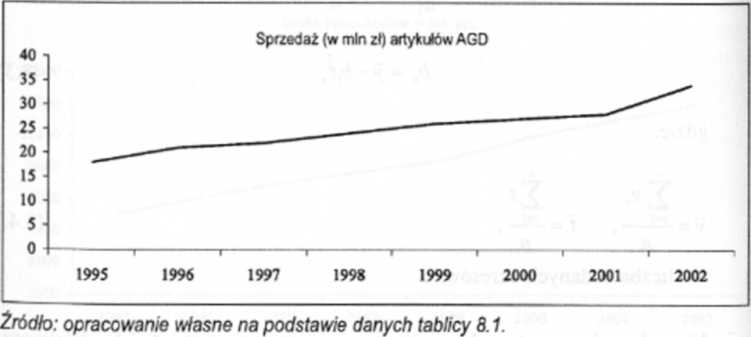
Poniższy szereg prezentuje dane dotyczące wielkości sprzedaży (w min zł) artykułów AGD w hurtowni A w latach 1995-2002.

Tablica 8.1. Sprzedaż (w min zł) artykułów AGD w hurtowni A w latach 1995-2002

Lata t	Sprzedaż w min zł Yt
1995	18
1996	21
1997	22
1998	24
1999	26
2000	27
2001	28
2002	34

Źródło: dane umowne.

Sporządź wykres tego szeregu w układzie współrzędnych (diagram czasowy). Wyznacz równanie funkcji trendu oraz oblicz przewidywaną wartość sprzedaży w roku 2004.

Wykreślenie diagramu czasowego znacznie ułatwi arkusz Excel. Jest to bowiem forma wykresu liniowego, którego sposób konstrukcji opisano w rozdziale 3.

W celu wyznaczenia funkcji trendu należy oszacować parametry równania (6, i b₀) korzystając ze wzorów 8.2 i 8.3. Wszystkie obliczenia będą wykonywane w tablicy 8.2. W celu ułatwienia obliczeń kolejne lata zastępujemy zmienną t = 1,2,...8, czyli np. rok 1995 = 1, rok 1996 = 2 itd. kończąc na 2002 roku, kiedy to t = 8.

Wykres 8.2 Diagram czasowy

Tablica 8.2. Obliczenia niezbędne do wyznaczenia parametrów równania linii trendu

t	y,	ty,	fi
1	2	3	4
1	18	18	1
2	21	42	4
3	22	66	9
4	24	96	16
5	26	130	25
6	27	162	36
7	28	196	49
8	34	272	64
1 = 36	1=200	1=982	1=204

Źródło: obliczenia własne na podstawie danych z tablicy 8.1.

W powyższej tablicy zostały wykonane niezbędne obliczenia do wyznaczenia parametrów funkcji trendu. Pierwsza kolumna oznaczona przez t to zmienna czasowa zastępująca kolejne lata. Druga kolumna to wielkości empiryczne czyli sprzedaż w min zł w kolejnych latach. Trzecia kolumna przedstawia iloczyn zmiennej t ■ y, (np. 5 • 26 = 130), a w ostatniej znajduje się wartość zmiennej t podniesiona do kwadratu. Jak możemy zaobserwować każda kolumna po wykonaniu odpowiednich obliczeń została zsumowana. Wszystkie powyższe obliczenia są niezbędne do wyznaczenia na podstawie formuły (8.2) współczynnika 6,:

36 200

OSO

. _    ₈    ,982-900 ^ 82 _₁₉₅

¹ w <³⁶>^{2    204}“^{162    42}    ’

8

Po oszacowaniu współczynnika b, możemy teraz przejść do wyznaczenia współczynnika b₀ na podstawie formuły (8.3). Aby rozpocząć ten proces musimy jednak wcześniej obliczyć średnie, zgodnie ze wzorami (8.4):

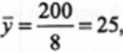
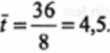
Po wyznaczeniu średnich możemy przejść do obliczenia wyrazu wolnego bp b₀ = 25-1,95 • 4,5 = 25 - 8,78 = 16,22.

Linia trendu dla sprzedaży sprzętu AGD w hurtowni A jest następująca: y,= 1,95/ + 16,22.

Na uwagę zasługuje tutaj interpretacja parametru b, zwanego współczynnikiem trendu. Ponieważ parametr ten jest dodatni b, > 0, oznacza to, iż sprzedaż artykułów AGD w badanej hurtowni w latach 1995-2002 średniorocznie wzrastała o 1,95 min zł.

219