30 31

Rozkład, którego krzywa liczebności (dla cechy ciągłej) lub diagram (dla cechy skokowej) ma jedno maksimum, nazywa się rozkładem jednomodalnwn Wśród rozkładów jednomodalnych można wyróżnić rozkłady symetryczne, umiarkowanie asymetryczne i skrajnie asymetryczne. W rozkładzie symetrycznym jednomodalnyin liczebności odpowiadające wartościom zmiennej rozkładają się symetrycznie wokół liczebności największej.

Rozkładem symetrycznym o jednym maksimum jest rozkład normalny. Rozkład ten ma szczególnie duże znaczenie w statystyce matematycznej, gdyż wiele cech różnych zbiorowości charakteryzuje się takim właśnie rozkładem (np. wzrost lub długość stopy). Należy podkreślić, że rozkład normalny jest rozkładem symetrycznym o ściśle określonej kurtozic, tzn. koncentracji wartości zmiennej wokół średniej arytmetycznej. Każdy rozkład normalny jest więc rozkładem symetrycznym, ale nie każdy rozkład symetryczny jest rozkładem normalnym. Na przykład rozkłady: platokurtyczny (spłaszczony) i lepkokurtyczny (wysmukły) są rozkładami symetrycznymi, ale nic normalnymi.

Rozkłady empiryczne o charakterze symetrycznym występują rzadko. Częściej spotykamy się z rozkładami zbliżonymi do rozkładu symetrycznego (asymetrycznymi). Rozkłady asymetryczne mogą być umiarkowanie asymetryczne i skrajnie asymetryczne, a te z kolei prawoskośne i lewoskośne. Rozkłady asymetryczne charakteryzują się tym, że prostopadła do osi odciętych poprowadzona z punktu maksimum krzywej liczebności dzieli powierzchnię pod krzywą na dwie nierówne części. Jeśli większa powierzchnia wraz z dłuższym „ramieniem" krzywej znajduje się po prawej stronie punktu maksimum, to rozkład jest prawoskośny. W przeciwnym razie mamy do czynienia z rozkładem lewoskośnym

Rozkłady mające tylko jedno „ramię” noszą nazwę skrajnie asymetrycznych. Są one rozkładami jednostronnymi względem wartości cechy o maksymalnej liczebności.

Niektóre cechy statystyczne mogą mieć rozkład będący niejako kompozycją dwóch rozkładów skrajnie asymetrycznych. Określa się jc mianem rozkładów L lub rozkładów siodłowych.

Jeśli krzywa liczebności lub diagram rozkładu ma dwa maksima, to rozkład taki nazywamy bimodalnym. Rozkłady mające więcej niż dwa maksima lokalne nazywamy wielomodalnymi.

Rozkłady symetryczne i umiarkowanie symetryczne charakteryzują

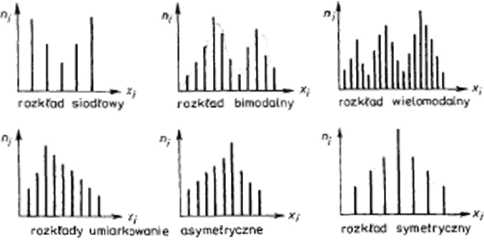
o/ <3ta cechy ciągłe;

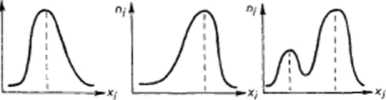
--^«i    ^^A!

rozkłady umiarkowanie asymetryczne rozktod bimodotny

rozktw) s>cdłow i

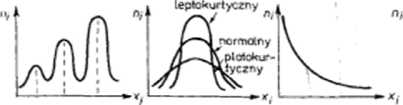
rozkład wielomodatny rozkłady symetryczne rozkłady skrajnie osymetryczne

Rys. 3. Przykłady podstawowych typów rozkładów empirycznych

31