Cwicz 4 5

Z równania tego należy policzyć dla każdego z ośmiu wykonanych pomiarów wartości doświadczalnego współczynnika oporów. Prędkość przepływu powietrza u [m/s] oblicza się z równania zwężki pomiarowej

u = 2,47

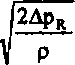
(4-14)

•    m    ♦    *    ^

gdzie Ap_R - ciśnienie różnicowe zmierzone manometrem 72 [Pa], p - gęstość

powietrza (podobnie jak w równaniu 4.13) [kg/m³].

Gęstość p można obliczyć z równania stanu dla powietrza

P =

P

287 T

(4.15)

gdzie p - ciśnienie absolutne powietrza [Pa], T - temperatura powietrza [K], 287 J/(kg-K) - indywidualna stała gazowa dla powietrza.

Można przyjąć, że ciśnienie przepływającego powietrza jest równe ciśnieniu atmosferycznemu (w rzeczywistości ciśnienie jest nieco większe), a jego temperatura jest równa temperaturze otoczenia. Gęstość powietrza można także odczytać z odpowiednich tabel dla ciśnienia i temperatury aktualnie panujących w laboratorium.

Dla każdego z ośmiu wykonanych pomiarów należy obliczyć wartość liczby Reynoldsa dla przepływającego powietrza (równanie 4.6) i literaturowy współczynnik oporów przepływu (z równania 4.5). Występującą w liczbie Reynoldsa lepkość powietrza należy odczytać z tabel dla temperatury otoczenia.

Obliczone i zebrane w tabeli wyników doświadczalne i literaturowe współczynniki oporów przepływu należy porównać ze sobą wyciągając wnioski co do dokładności pomiarów.

Rura z zaworem. Dla każdej z badanych rur z zaworem strata ciśnienia wynika z oporu tarcia i oporu miejscowego i zgodnie z równaniem (4.1) jest równa zmierzonemu spadkowi ciśnienia na odcinku poziomym (Apa ~ Apt + Ap_m= Ap). Współczynnik oporu miejscowego ę oblicza się z równania

Wielkość współczynnika oporów przepływu X należy obliczyć z równania (4.5), zaś prędkość przepływu powietrza jak dla rury prostej. Długość zastępczą dla zaworu należy obliczyć z równania (4.9). Obliczenia te wykonuje się dla każdej z dwóch prędkości, dla których wykonano doświadczenia.

Rura z rozszerzeniem przekroju. Podczas przepływu powietrza rurą z rozszerzeniem przekroju strata ciśnienia wynika z oporów tarcia w dwóch odcinkach rury o różnych średnicach oraz z oporu miejscowego związanego z rozszerzeniem przekroju (Ap^ =Ap_tI + Ap_t2 +Ap_m). Jednocześnie ze względu na różne prędkości przepływu powietrza w każdym z odcinków badanej rury, strata ciśnienia nie jest równa zmierzonemu spadkowi ciśnienia. Równanie (4.1) może być rozwinięte i przekształcone do postaci

. Uj ^uf . Ap = -^-p--J-_{p +} x

L, uf , d, 2 ^v 2

L, uf „uf

z-f^p+ęt^p <⁴-^,7>

Z równania tego należy obliczyć współczynnik oporu miejscowego ę dla rozszerzenia przekroju.

Równanie zwężki (4.14) pozwala obliczyć prędkość gazu u₂ w przekroju większym (o średnicy d₂). Prędkość gazu w przekroju mniejszym (o średnicy d,) należy obliczyć z zależności

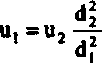
W oparciu o te wielkości należy obliczyć wartość liczby Reynoldsa dla obu przekrojów oraz współczynniki oporów przepływu X, i X₂ z równania (4.5). Pozwala to w konsekwencji na obliczenie £ z równania (4.17). W celu porównania wyznaczonego doświadczalnie współczynnika oporu miejscowego dla rozszerzenia przekroju z wartością teoretyczną należy obliczyć go również zrównania (4.12). Długość zastępczą dla tego oporu obliczyć z równania (4.9). Obliczenia wykonuje się dla każdej z dwóch prędkości, dla których wykonano doświadczenia.

Rura z kolankami. Strata ciśnienia podczas przepływu powietrza rurą z kolankami wynika z oporów tarcia oraz czterech oporów miejscowych i jest równa zmierzonemu spadkowi ciśnienia (Ap^ = Ap_t + 4Ap_m = Ap).

Współczynnik oporu dla kolanka należy obliczyć z zależności