Str 055

stalowe ocynkowane,	— zwyczajne	0,140,15
żeliwne	— nowe	0,25-rl,0
	- w eksploatacji	1,041,5
betonowe i żelbetowe,	— średnio gładkie	2,5
azbestocementowe	— w eksploatacji	0,6

W praktyce inżynierskiej spotykamy się najczęściej z następującymi typami zadań dotyczących obliczania przewodów pojedynczych:

I. Znane są: wymiary przewodu (d, L) i jego chropowatość (k), lepkość cieczy (v) oraz natężenie przepływu (Q). Należy obliczyć różnicę ciśnień na końcach odcinka przewodu, co sprowadza się do obliczenia strat energii h_s na tym odcinku.

U. Znane są: wymiary przewodu (d, L) i jego chropowatość (fc), lepkość (v) i straty (fij. Należy obliczyć natężenie przepływu w przewodzie Q.

HI. Znane są: długość przewodu (Z), jego chropowatość (k), lepkość (v), natężenie przepływu (Q) i wysokość strat energii h_s. Zadanie polega na doborze średnicy przewodu d, gwarantującej założony przepływ przy stratach nie przekraczających zadanej wartości h_s.

Przy rozwiązywaniu powyższych zadań dysponuje się następującym zestawem równań:

1) równaniem Bernoulliego dla strumienia cieczy rzeczywistej

Pi

Y 2g

P2 ^av2

h ⁺ — ^{+    +}

Y 2g pozwała ono na określenie h_s, jeżeli w zadaniu występują rzędne (z) i ciśnienia (p) oraz umożliwia sprowadzenie bardziej złożonych zadań do jednego z podanych wyżej typów;

2) równaniem Darcy’ego-Weisbacha i wzorem na stratę lokalną

h

S

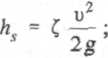
3)    wzorami na współczynnik oporów liniowych X zależnymi od strefy ruchu. W praktyce w celu określenia wartości X posługujemy się wykresem Colebrooka-White’a, współczynnik oporów liniowych zależy od

_n vd    k

v    d

4)    równaniem ciągłości

Q = Fu =    = const.

4

Pierwszy rodzaj zadań polegający na wyznaczeniu strat jest najprostszy i daje się rozwiązać przez proste wykorzystanie podanych równań. Za pomocą

55