P1080230

4. Wprowadzenie do kinematyki robotów

staci jawnej. Gdy jest to niemożliwe, wykorzystuje się metody numeryczne oparte na odwracaniu jakobianów i metodzie Newtona-Raphsona.

Zagadnienie to wykracza poza obszar tematyczny tej książki, a dokładniejsze omówienie zagadnienia kinematyki manipulatorów znajdzie Czytelnik w następujących pozycjach literatury: [21,36, 86, 124,130].

4.3. Kinematyka robotów o strukturach równoległych

4.3.1. Kinematyka manipulatora równoległego typu DELTA

Na rysunku 3.32 pokazano strukturę kinematyczną manipulatora równoległego (tripoda) typu DELTA.

Zadanie proste manipulatora równoległego typu DELTA polega na wyznaczeniu pozycji członu roboczego określonej współrzędnymi: xp, yp, zp, które są funkcją trzech zmiennych konfiguracyjnych: <%, a_2i a^. Schemat manipulatora typu DELTA opisujący wielkości geometryczne przedstawiono na rys. 4.21.

Niech Qi (i = 1, 2, 3) oznacza punkt w przestrzeni, powstały na skutek przesunięcia punktu C, równolegle do wektora BjV (linia przerywana), przy czym VQi = l₂ [86]. Podstawą wyznaczenia współrzędnych xp, y_P, z_P jest znalezienie współrzędnych geometrycznych x_Ut yu, ^zu, teoretycznego punktu U leżącego na prostej prostopadłej do płaszczyzny wyznaczonej przez punkty B\_% B₂, Bi członu roboczego. Współrzędne xy, yu, zy wyznacza się w przestrzeni jako punkt przecięcia trzech płaszczyzn: ni - płaszczyzny symetrii odcinka QiQ:, Ki - płaszczyzny symetrii odcinka Q\Qi oraz ni — płaszczyzny punktów Q,_y rozważając układ zamknięty złożony z trzech ramion robota przedstawionych na rys. 4.21.

QlQ2 *Q\Q) •

Korzysta się z postaci ogólnej równania płaszczyzny wyznaczonej przez dowolny punkt na niej leżący oraz współrzędne dowolnego wektora normalnego. Zgodnie z tym, opierając się na współrzędnych punktów xq, , yę,, z_Ql (i = 1, 2, 3), wyznacza się równania płaszczyzn n\ i ni leżących na punktach określonych jako środki symetrii odcinków Q\Qi i Q\Qi oraz prostopadłych do wektorów Q\Qi,Q\Qi utworzonych przez te odcinki. Równanie płaszczyzny ny można wyznaczyć np. opierając się na współrzędnych punktu Q\ oraz współ-rzędnych wektora normalnego wyznaczonych przez iloczyn wektorowy postaci:

Aby otrzymać współrzędne geometryczne x_a, y_Ut z_v punktu U, należy rozwiązać układ równań utworzony przez równania płaszczyzn jt\, n₂ i n₃, którego postać ogólna jest następująca

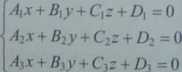
(4.49)

Di = -A/x_0l - Biy_0l - CiZo,

0/ są

gdzie

przy ezym A_h B_h Ci - są współrzędnymi wektora normalnego, a x_0ny współrzędnymi geometrycznymi wspólnymi z płaszczyzną.

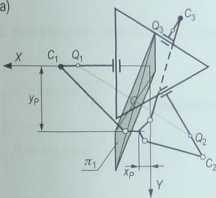
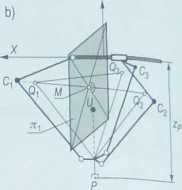
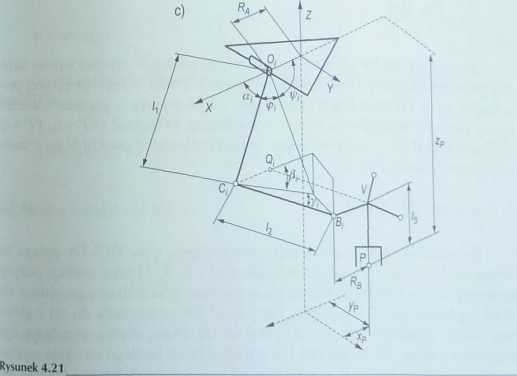
Schemat manipulatora typu DELTA: a) widok z góry, b) widok z boku, c) schemat jednego ramienia układu; l\ — długość ramienia, /₂ - długość członu równolegloboku, /₃ - odległość środka członu roboczego od środka platformy, a, - zmienny kąt obrotu i-tego ramienia, Pt - kąt między płaszczyzną /-tego równolegloboku a płaszczyzną podstawy mierzony w płaszczyźnie pionowej, zawierającej i-te ramię, - kąt między płaszczyzną pionową /-tego ramienia a członem równolegloboku, ,\>, y_P, z_f - współrzędne przemieszczenia członu roboczego [86]

107