Image52 (16)

191 Rozwiązania zadań ze zbioru "MENDLA

Zadanie 692 str.138

Szukane:

P2, Vi, V3

Dane:

n = 1 mol

pi = 1 MPa = 1000000 Pa Ti = 390 K

AU = -7,17 kJ = -7M0 J W = - 745 J

c_v = 21,63 R = 8,31

mol■ K J

K ■ mol

Z równania gazu doskonałego Clapeyrona otrzymamy:

= n • R /• Ti Ti

n • R • Ti

pi • Vi = n ■ R • Ti    —^    Vi =

Pi

Najpierw gaz poddano przemianie izochorycznej, V = const, oraz V2 = Vi.

Z I zasady termodynamiki wiadomo, że

AU = Q + W , ale W = 0 stąd Q = AU ,    lecz    Q = c_v • n • AT

AU = c_v • n • (T2-T1)    /: c_v • n

AU

więc praca Wi = 0

AT = T₂ - Ti

T₂-Ti = T2 = Ti +

c_v • n AU

c_v • n

Zgodnie z prawem przemiany izochorycznej:

Pl ₌ P2

Ti T2

P2 =

P1 • T2

P1

stąd p2 =

^ AU

Ti +-

c_v • n

P2 = pi

; Ti

1 +

AU

c_v • n • Ti

Obliczymy teraz liczbowe ciśnienie p2 i objętość Vi.

-7170 J

P2 = 1 MPa

1 +

21,63

K ■ mol

1 mol ■ 390 K

p₂ = 1 MPa ■ (1 - 0,85) p₂ = 0,15 MPa = 150 kPa

vi=n^i

Pi

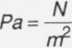
1 mol • 8,31 ~--y 390 K y,___K • mol_

¹ “    1000000 Pa    ’ ^{J =}

V1 = 0,00324-^^

N

rr?

Vi = 0,00324m³ = 3,24 dm³

Ze stanu 2 do 3 gaz przeszedł rozprężając się izobarycznie p = const, więc wykonaną pracę W wyrazimy:

W = - p • AV , ale aV = V3 - M2

stąd W = - p2 • (V3 - V2)

Przekształcając ostatnie równanie wyznaczymy końcową objętość gazu Mz.

W = - p2 • V3 + p • V2

P2 • V3 = P2 • V2 - W /: P2

w w W , _{w w} n • R • Ti

V3 = V2-— , lecz V2 = Vi=-

P2    P1

oraz p2 = pi

1 +

AU

c_v • n • Ti

Po podstawieniu:

n • R • Ti

V₃ =

W

Pi

P1

V₃ = 3,24 dm³ -

1 +

AU

-745 J 150 kPa

c_v • n • T1

J= N- m

Pa-

_N_

m²

V₃ = 3,24 drr? + 0,00497-^p

m²

V₃ = 3,24 dm³ + 4,97dm³ V3 = 8,21 dm³

Odp.: Objętość początkowa gazu wynosi 8,21 dm³. Ciśnienie gazu po przemianie izochorycznej wynosiło 150 KPa.

13 — Zeszyt 5