img294 (7)

Tablica 38

Surowce	Zużycie surowca (w kg) na 1 szt. wyrobu		Zapas surowca (kg)
	W,	W2
Sr	2	1	1000
S2	3	3	2400
s3	1,5		600
Cena (zł)	30	20

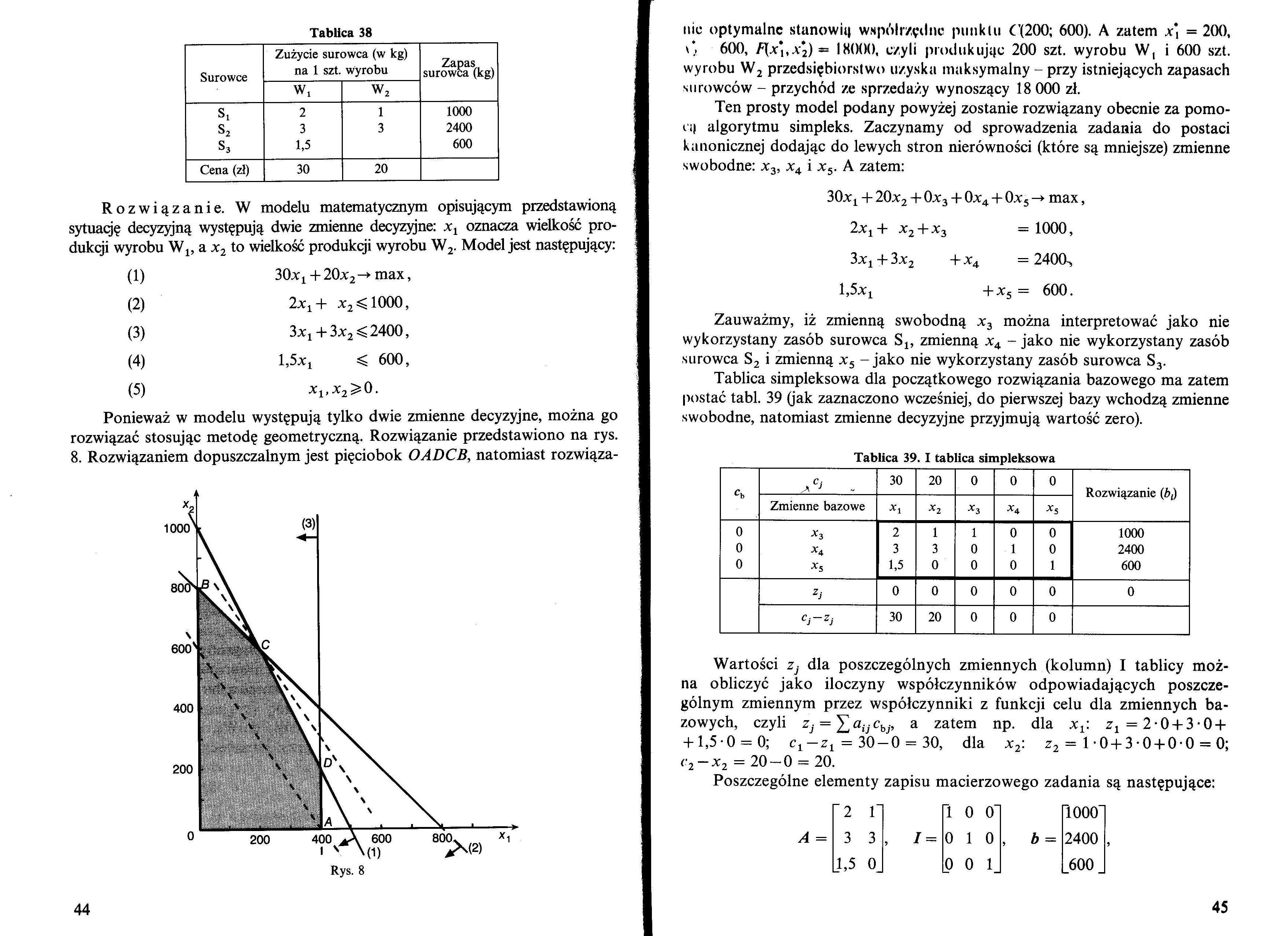
Rozwiązanie. W modelu matematycznym opisującym przedstawioną sytuację decyzyjną występują dwie zmienne decyzyjne: x_x oznacza wielkość produkcji wyrobu W_1; a x₂ to wielkość produkcji wyrobu W₂. Model jest następujący:

(1)	30^! + 20x2-> max,
(2)	2xt+ x2<1000,
(3)	3x1 + 3jc2<2400,
(4)	l,5xj ^ 600,
(5)	xltx2^0.
Ponieważ w modelu występują tylko dwie zmienne decyzyjne, można go rozwiązać stosując metodę geometryczną. Rozwiązanie przedstawiono na rys. 8. Rozwiązaniem dopuszczalnym jest pięciobok OADCB, natomiast rozwiąza-

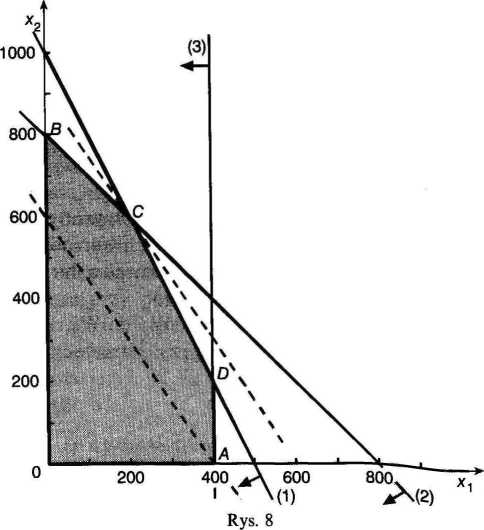
nic optymalne stanowił) współrzędne punktu ('(200; 600). A zatem x\ = 200, 0    600,    = 18000, czyli produkując 200 szt. wyrobu W, i 600 szt.

wyrobu W₂ przedsiębiorstwo uzyska maksymalny - przy istniejących zapasach surowców - przychód ze sprzedaży wynoszący 18 000 zł.

Ten prosty model podany powyżej zostanie rozwiązany obecnie za pomocą algorytmu simpleks. Zaczynamy od sprowadzenia zadania do postaci kanonicznej dodając do lewych stron nierówności (które są mniejsze) zmienne swobodne: x₃, x_A i x_s. A zatem:

30;^ + 20x₂ + 0x₃ + 0x₄ + 0x₅ -> max,

2x_x + x₂ + x₃    = 1000,

3*! + 3x₂    +x₄    = 240G,

l,5x_t    T x₃ = 600.

Zauważmy, iż zmienną swobodną x₃ można interpretować jako nie wykorzystany zasób surowca S_1? zmienną x₄ - jako nie wykorzystany zasób surowca S₂ i zmienną x₅ - jako nie wykorzystany zasób surowca S₃.

Tablica simpleksowa dla początkowego rozwiązania bazowego ma zatem postać tabl. 39 (jak zaznaczono wcześniej, do pierwszej bazy wchodzą zmienne swobodne, natomiast zmienne decyzyjne przyjmują wartość zero).

Tablica 39. I tablica simpleksowa

	a^c; -	30	20	0	0	0	Rozwiązanie (bt)
	Zmienne bazowe	A,	x2	*3	*4	x5
0	*3	2	1	1	0	0	1000
0	*4	3	3	0	1	0	2400
0	*5	1,5	0	0	0	1	600
		0	0	0	0	0	0
	^ci ~^zi	30	20	0	0	0

Wartości z_} dla poszczególnych zmiennych (kolumn) I tablicy można obliczyć jako iloczyny współczynników odpowiadających poszczególnym zmiennym przez współczynniki z funkcji celu dla zmiennych bazowych, czyli Zj = Y_ja_ijc_bj, a zatem np. dla x{. z_x =2-0 + 3-0 + + 1,5-0 = 0; c_x —z_x = 30—0 = 30, dla x₂: z₂ = 1 -0 + 30 + 0-0 = 0; c₂ —x₂ = 20 —0 = 20.

Poszczególne elementy zapisu macierzowego zadania są następujące:

	~ 2 r		1 0 0'		1000'
A =	3 3	, / =	0 1 0	, b =	2400
	1,5 0,		0 0 1.		.600.

45