img444 (2)

Omówimy jeszcze jedno ważne twierdzenie dotyczące funkcji ciągłych.

TWIERDZENIE 11 . (o lokalnym zachowaniu znaku)

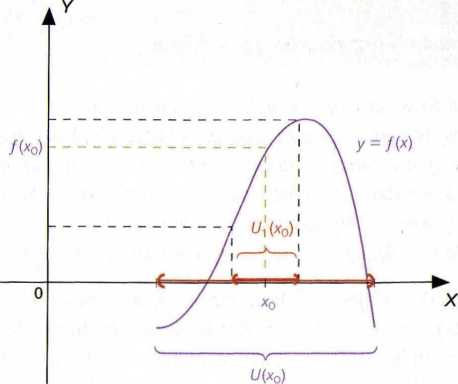
Jeżeli funkcja / określona w pewnym otoczeniu U(x₀) punktu x₀ jest ciągła w punkcie x₀ oraz f{x_Q) > O (odpowiednio f{x₀) < O), to istnieje takie otoczenie U_A {x₀) punktu x₀, że U_: (x₀) a U(x₀) oraz f{x) > 0 (odpowiednio /(x) < O) dla każdego xel/₁ (x₀).

Dowód tego twierdzenia pominiemy. Jego ilustrację (dla przypadku f(x₀) > O) przedstawia poniższy rysunek:

Ciągłość funkcji w przedziale liczbowym

W poprzedniej części wykazaliśmy, że funkcja /(x) = a^x, a > 0 jest ciągła w każdym punkcie x₀ e R. Możemy powiedzieć, że jest ona ciągła w zbiorze liczb rzeczywistych lub że jest ciągła w przedziale (-qo, +oo). W ogólnym przypadku możemy zatem przyjąć następującą definicję:

OEfINICJA 11.

Funkcja / jest ciągła w przedziale otwartym (o, b) wtedy i tylko wtedy, gdy jest ciągła w każdym punkcie tego przedziału.

iii

liłię trudniej zdefiniować ciągłość funkcji w innych przedziałach. Zacznijmy |ir/*d/lału domkniętego. Niech np. /(x) = x - 2, xe (1, 3). Wykres tej funk-pl/mhlawiono poniżej:

m

«|i

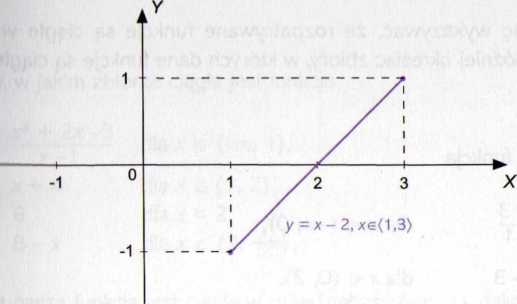
W każdym punkcie przedziału (1,3) funkcja ta jest na pewno ciągła. Widać ponadto, że dodatkowo funkcja ta jest prawostronnie ciągła w punkcie #i,    1 (ponieważ lim /(x) = /(1), a o granicy lewostronnej w tym punkcie

file można mówić) oraz lewostronnie ciągła w punkcie x₀ = 3 (ponieważ IIjjj ,f(x) = /(3), a o granicy prawostronnej w tym punkcie nie można mówić).

Ogólnie więc możemy przyjąć definicję:

1BIMCJA12.

Funkcja / jest ciągła w przedziale domkniętym (a, b), jeśli jest ciągła w przedziale (o, b) oraz jest prawostronnie ciągła w punkcie x₀ - a i lewostronnie Ciągła w punkcie x₀ = b.

Utwo teraz już określić, co będziemy rozumieć przez ciągłość funkcji w innych przedziałach liczbowych (sformułuj odpowiednie definicje!).

Na koniec powiemy, że funkcja / jest ciągła w zbiorze będącym sumą kilku przedziałów liczbowych, jeśli jest ciągła w każdym z tych przedziałów. Oczywiście, jeśli funkcja jest ciągła w pewnej liczbie przedziałów, to jest również ciągła w zbiorze będącym sumą tych przedziałów. Na przykład funkcja /(x) =

w i O

-—j- jest ciągła w każdym z przedziałów (-oo, 1) oraz (1, +oo), jest więc leż ciągła w zbiorze (-oo, 1) u (1, +oo).