img508 (3)

20. Niech g m lim ⁽"    ¹ *, a e N Wówczas:

*■ ^M“ 2 + (« - I)jc

□    a) & jest skończona dla dowolnego a e R,

□    b) g < 1 wtedy i tylko wtedy, gdy a < 0,

□    c) jeśli |a | = 1, to g = 0.

Pochodna fu n kej i

1. Funkcja / jest dowolną funkcją różniczkowalną w zbiorze R {1}, malej dziale (-00, 1) oraz rosnącą w przedziale (1, +00). Wynika stąd, że:

□    a) / ma minimum lokalne w punkcie x₀ = 1,

□    b)jeśli/'(2)*0 oraz /'(0)*0,to f'(2)>f'(0),

□    c) f'{x)>0 dla dowolnego x e (1, +00).

2. Rozważmy funkcję f(x) =

a(x +1) dla x < 0

x² + a dla x >0

, a e R. Wówczas:

□    a) funkcja / jest ciągła dla dowolnego a e R,

□    b) jeśli a = 1, to funkcja / jest różniczkowalna w zbiorze R,

O c) istnieje liczba a e R, dla której funkcja / jest różniczkowalna w zbioi.

3.    Niech f{x) = {    .Wówczas:

\2x -1 dla x > 1

C] a) funkcja / nie jest różniczkowalna w punkcie x₀ = 1,

C] b) funkcja / ma w punkcie x₀ = 1 minimum lokalne,

CD c) funkcja / jest rosnąca w przedziale (0, + co)

4.    W stożek o promieniu podstawy długości 5 i wysokości 20 tak wpisano w dolna podstawa jest zawarta w podstawie stożka, a oś symetrii walca pokrywa metrii stożka. Funkcja V(r), wyrażająca objętość walca w zależności od długo? jego podstawy spełnia warunki:

3

[H a) ma maksimum lokalne dla r = —,

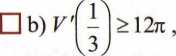
□ c) jest ciągła w przedziale (0, 5).