MATEMATYKA054

]()() HI. Rachunek różniczkowy

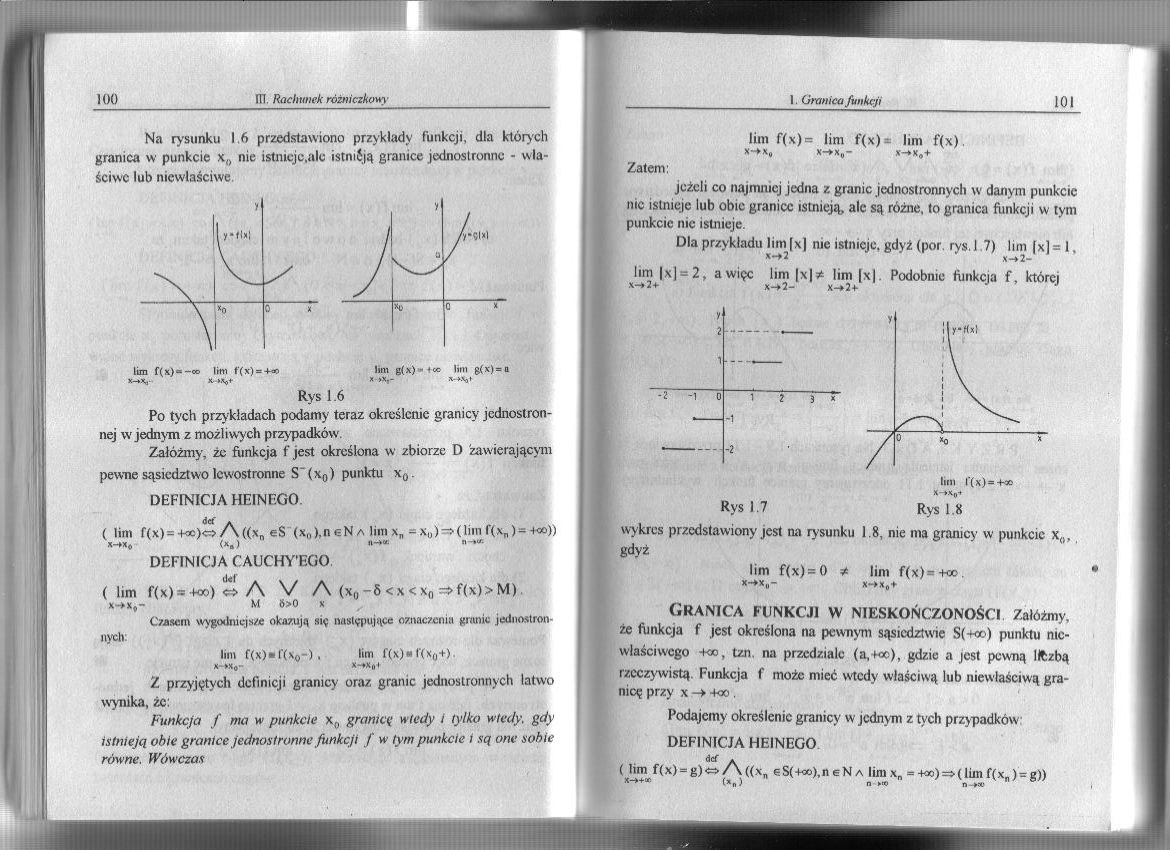
Na rysunku 1.6 przedstawiono przykłady funkcji, dla których granica w punkcie x₀ nie istnieje,ale istmiją granice jednostronne - właściwe lub niewłaściwe

]()() HI. Rachunek różniczkowy

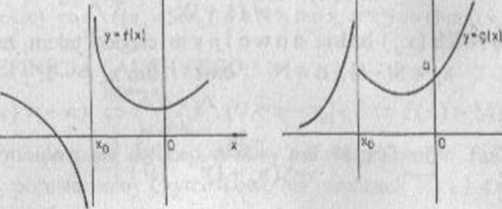
lun f(x)«-oo lim f(x)»-Ho

lim g( x) * «oc lim g( x) = a

Rys 1.6

Po tych przykładach podamy teraz określenie granicy jednostronnej w jednym z możliwych przypadków.

Załóżmy, że funkcja f jest określona w zbiorze D zawierającym pewne sąsiedztwo lewostronne S~(x₀) punktu x₀.

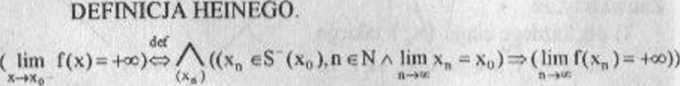
DEFINICJA CAUCHY EGO.

(lim f(x) = 4oo) <=> A V A (x₀-ó <x<x₀ =>f(x)>M)

x->x₀-    M 6>0 x

Czasem wygodniejsze okazują się następujące oznaczeniu granic jednostron-

nych:

x-»x₀-

lim f(x)al'(XQ+).

X~*Xfll

Z przyjętych definicji granicy oraz granic jednostronnych łatwo wynika, że:

Funkcja f ma w punkcie x₀ granicę wtedy t tylko wtedy, gdy istnieją obie granice jednostronne funkcji f w tym punkcie i są one sobie równe. Wówczas

lim f(x)« lim f(x)* lim f(x).

X“>X_#    X-»Xg-    X-*Xg +

Zatem:

jeżeli co najmniej jedna z granic jednostronnych w danym punkcie nic istnieje lub obie granice istnieją, ale są różne, to granica funkcji w tym punkcie nic istnieje.

Dla przykładu lim|x] me istnieje, gdyż (por. rys. 1 7) lim fx] = I _%

x-t2    x-*2-

lim |x) = 2, a więc lim |x|^ lim (x|. Podobnie funkcja f, której

x-»2+    x-»2-    x-*2 +

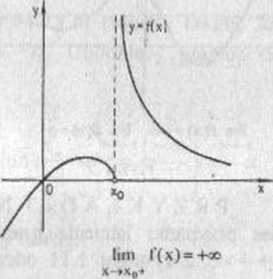
Rys 1.7    Rys 1.8

wykres przedstawiony jest na ry sunku 1.8, nie ma granicy w punkcie X₀, gdyż

lim f(x)=0 * lim f(x)=+oo.

x-»x„-    x-»x_#*

Granica funkcji w nieskończoności, załóżmy, że funkcja f jest określona na pewnym sąsiedztwie S(+oo) punktu niewłaściwego +co, Un. na przedziale (a,+oc), gdzie a jest pewną llfczbą rzeczywistą. Funkcja f może mieć wtedy właściwą lub niewłaściwą granicę przy x -> +oo .

Podajemy określenie granicy w jednym z tych przypadków DEFINICJA HEINEGO

der _A

( lim f(x) = g)«=>/\((x_n €S(-ko),u eN a lim x_n --foo)=^(liin f(x_n) = g))

x-*+»    {*,)    n ►*>    «-**