Nowy 3 (7)

224 12. Szybkie przekształcenie Fou

Numery próbek    Numery próbek

w normalnej kolejności    po odwróceniu bitowym

Dziesiętne	Binarne	Dziesiętne	Binarne
0	0000	0	0000
1	0001	8	1000
2	0010	4	0100
3	0011	12	1100
4	0100	2	0010
5	0101 ,—	-\ 10	1010
6	0110	1 ^6	0100
7	0111	14	1110
8	1000	1	0001
9	1001	9	1001
10	1010	5	0101
11	1011	13	1101
12	1100	3	0011
13	1101	11	1011
14	1110	7	0111
15	1111	15	1111

Rys. 12.3. Sortowanie z odwróceniem bitowym w FFT. Rozkład FFT w dziedzinie czasu można wykona: przez posortowanie próbek zgodnie z odwróconą kolejnością bitów

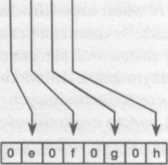
towych z użyciem przeplotu. Rozpatrzmy dwa sygnały w dziedzinie czasu, abcd oraz Sygnał 8-punktowy w dziedzinie czasu może być utworzony w dwóch krokach: rozrz zerami każdego 4-punktowego sygnału, aby uczynić z niego sygnał 8-punktowy i nas zsumowanie uzyskanych sygnałów. To znaczy, że sygnał abcd staje się sygnałem aO a efgh staje się sygnałem OeOfOgOh. Zsumowanie tych dwóch 8-punktowych sygnałów twarza sygnał aebfcgdh. Jak wynika z rys. 12.4, rozrzedzanie zerami sygnału w dzie czasu jest powielaniem widma częstotliwościowego. Zatem w FFT widma częstotliwo' są łączone ze sobą przez ich powielanie i następnie sumowanie powielonych widm.

Dziedzina czasu

Dziedzina częstotliwości

(UZĘB

Rys. 12.4. Synteza FFT. Rozrzedzanie zerami sygnału w dziedzinie czasu powoduje powielanie widma w dziedzinie częstotliwości. Jeśli sygnał w dziedzinie czasu jest podczas rozrzedzania także przesunięć o jedną próbkę, to widmo będzie dodatkowo pomnożone przez sinusoidę