skan0043

100

2.12. Zastosowanie przekształcenia Laplaco^n

Traneformatę Laplace’a można stosować do rozpisywania zagadnień początku* wyoh dla liniowych równań różniczkowych zwyczajnych o współczynnikach stałych, Jak 1 układów takich równań. W tym celu należy zastosować wzór na transformatą n' tuj pochodnej:

£[l/⁽"⁾W] = sⁿ>'«-£sⁿ-'7^<‘-¹⁾(0), gdzie y(s) = £&,(*)],    (2.12.1)

k=l

W tabeli transformat Laplace’a umieszczono szczególne przypadki tego wzoru dla n w 1 oraz n = 2.

Wyznaczyć rozwiązania zagadnień początkowych:

1.    y" + 4y = 8 sin 2t, y(0) = 0, y'(0) = 2

2.    y"'-y"-y'+y = 6e*, y(0) = y'(0) = y"(0) == 0

a stąd

Y(s)-

2 s¹ + 24 (s¹ + 4)¹ ’

Należy teraz wyznaczyć transformatę odwrotną funkcji F. W tym celu funkcję I^{2 3}' rozłożymy na ułamki proste, a więc

2a¹ + 24 Aa | li Ca -|- D (a¹ + 4)^a " T* I 4 * ^ 4- 4)^a

czyli

2# i 24 w (/U I | 4) 4- Ca Śj1),

Porównując współczynniki przy tych samych potęgach a, mamy następujący układ równań na wyznaczenie stałych A i B :

a°    24 = 4 B + D

a    0 = 4 A + C

s⁴    2 = B

s³ 0=4

Stąd A = C — 0, B = 2, D = 16, a więc

' 2a^4 + 24'	/»-i	' 2 '	+£-^ł	16
(a^4 + 4)^4 j	— L*	a^44-4j		(a^4 + 4)^4

= sin2i+£ ¹

16

(a⁴+4)⁴

Ponieważ

stąd

a więc

1    _ a⁴ — 4 a⁴ + 4    9

(s⁴+4)⁴ “ (a⁴ + 4)⁴ “ (a⁴Ti)^{2 +} (s⁴ + 4)⁴ ’

8    . a⁴-4    1

(a⁴ + 4)⁴ ~ (s⁴ + 4)2 s⁴ + 4’

Z powyższych obliczeń wynika

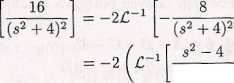
(a² + 4)²

= —2 cos 21 — ^ sin 2tj

s⁴ + 4_

2t cos 2i + sin 2t

l' ⁵    m f*fjs= f /(t-r)g(r)dr.

J o

Transformatę odwrotną £ ⁵ twierdzenia Borola o splocie:

16

(a⁴+ 4)⁴

można również obliczyć korzystając z

1

Korzystając z warunków początkowych, można powyższe wyrażenie przedstawić w postaci

2

Rozwiązania

3

Stosując przekszałcenie Laplace’a do równania różniczkowego i korzystając zo wzoru (2.12.1) dla n = 1 oraz n.= 2, otrzymamy:

*-Y(s)    = 8^-r.

8* + 4

4

2/(i) = 2 sin 2t — 21 cos 2i.

5

stąd szukane rozwiązanie jest postaci: