str144 (4)

144

3. PRZEKSZTAŁCENIE LAPLACE'A I JEGO PEWNE ZASTOSOWANIA

§ 2. WYZN

Własność 12 (przesunięcie obrazu). Jeżeli L [/(/)] = #(0> ^t0 (1.14)    L[e^|,°7(0] = 4>(s-Po),

gdzie p₀ jest dowolną liczbą zespoloną.

Własność 13. Dla dowolnego oryginału f(t) i jego obrazu (s) prawdziwy jest związek graniczny

lim /(t) = lim s4> (s).

l-*0-f-0    s-+oo

Własność 14. Jeżeli istnieje granica oryginału /(/), gdy t-*co, to

lim f(t) = lims4>(s),

*-*oo    s-*0

gdzie <P(s) jest obrazem Laplace'a funkcji f(t).

§ 2. Wyznaczanie obrazu (transformaty Laplace’a), gdy znany jest jego oryginał

Najprostszą funkcją-oryginałem jest funkcja jednostkowa t\{t) określona wzorem (rys. 3.2):

rl    dla    t> O,

(O    dla    t< 0.

Rys. 3.2

Przypuśćmy teraz, żeę(t) jest dowolną funkcją, która spełnia warunki 1° i 3° definicji 1, § 1, ale nie spełnia warunku 2° tej definicji. Łatwo zauważyć, że funkcja /(/) określona wzorem

/(O = *;(0 ^>(0 =

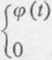
dla

dla

t>0,

t<0

czyni zadość również warunkowi 2°, czyli jest oryginałem (np. i/(/)sint, jj (/)/", )] (t)e^at).

Uwaga 1. Umawiamy się, że w dalszym ciągu (dla prostoty zapisu) będziemy zawsze wszystkie rozpatrywane funkcje traktować jako równe zeru dla /<0. Na przykład zamiast t](t) będziemy pisać 1, zamiast ą(f)e^xt— po prostu e^xt.

Zadania przykładowe

Zadanie 2.1. Znaleźć obra Rozwiązanie. Stwierdza ność (1.1) spełnia ona ze stałą wzoru (1.2). Przyjmując w t; Re^ = /. > /₀ = O

n

czyli obraz funkcji jednostko!

Zadanie 2.2. Znaleźć obra; rzeczywistą.

Rozwiązanie. Stwierdzan spełnia ona ze wskaźnikiem ź₀ w którym /(/) = e^al, mamy

m

0

bo wobec A>a mamy dla t-> oo. Zatem

gdzie a to dowolna liczba rze Zadanie 2.3. Znaleźć obra Rozwiązanie. Stwierdzan rzędu wykładniczego o wskaż

wzoru (1.2) zastosowanego dc

00

4>(s) = Jsin6te^_1,i

o

bo wobec 2>0 mamy kolejne e~^a

-=-, (-ssin bt

s² + b²

10 — Wybrane działy matematyki...