S6303022

416 HYDRAULIKA TECHNICZNA. PRZYKŁADY OBLICZEŃ

natury niż wymiary samego modelu. Jeszcze bardziej maleją oczywiście natężenia przepływu.

Przypuśćmy, że wykonano model obiektu hydrotechnicznego dziesięciokrotnie mniejszy,

•    • .    _#    v ii*

a więc w skali liniowej ct_L =1/10. Jeśli skala prędkości jest równa oc_v =~ = cł, to

v

znaczy, że prędkość na modelu winna być równa v = v'a^^/2 = v'* ^/5T « 0,32v', czyli że byłaby ona tylko trzykrotnie mniejsza niż w naturze. Skala przepływu natomiast jest

równa ct₀ = — = a^⁵, co oznacza, że przepływ modelowy powinien być równy

Q — Q^łOL]f = Q' 0,1^{2 5} =0,00320' i stanowi w przybliżeniu zaledwie 3%o przepływu naturalnego (czyli przepływowi np. 1 m³/s w naturze będzie odpowiadać około 3 1/s na modelu).

Przy zastosowaniu kryterium Froude’a otrzymuje się skale różnych wielkości związanych z ruchem cieczy w zależności od obranej skali geometrycznej modelu przy stosowaniu tej samej cieczy w naturze i do badań na modelu.

W praktyce oznacza to możliwość modelowania pracy budowli wodnych w laboratorium z wykorzystaniem wody. Należy jednak zdawać sobie sprawę kiedy można stosować liczbę Froude’a jako kryterium podobieństwa przy zachowaniu dostatecznej dla praktyki dokładności, gdy pomija się poza siłami ciążenia wpływ działania innych sił.

Kryterium Froude’a można stosować do modelowania przepływów o swobodnym zwierciadle wody, a więc w korytach otwartych, przelewach i innych budowlach hydrotechnicznych, spełniających wymieniony warunek.

Podobieństwo sił tarcia — kryterium Reynoldsa

Polega ono na tym, że jako dominujące w modelowanym zjawisku przyjmuje się (poza siłami bezwładności) siły tarcia, czyli siły powiązane bezpośrednio z lepkością cieczy. Przedstawiając siłę tarcia w cieczy jako iloczyn naprężenia stycznego T i powierzchni A jej występowania, a także uwzględniając tzw. model lepkości Newtona (rys. 15.1), można napisać:

płytka

o powierzchni A

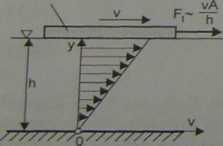
F, = xA=pA-^-    (15.25)

dy

gdzie:

.    .    ,    , dv.

t — naprężenia styczne (x = ±jx—),

dy

p — dynamiczny współczynnik lepkości cieczy [Ns/m j, v — prędkość przesuwania płytki leżącej na nieruchomej cieczy [m/s],

y — odległość płytki od dna (czyli wymiar liniowy) [mj.

RYSUNEK 15.1. Model lepkości cieczy podany przez Newtona

Projektowanie parametrów geometrycznych i hydraulicznych fizycznego modelu 417

.2 dv v .    ___ . i .    ., £ .    ,

Ponieważ A = L oraz —=—, więc można zapisać, że siły tarcia są równe: dy L

F, -—=\iLv    (15.26)

Skalę sił tarcia na modelu i w naturze wyraża wtedy stosunek:

F, uLv

^arF;“ji'/,v‘ ^M 1 v Skala sił tarcia musi spełniać warunek ogólny podobieństwa dynamicznego, to znaczy równości skal sił tarcia i sił bezwładności: pjLv

(15.27)

p LV

(15.28)

|i'LV p'L'V²

Po redukcji i uwzględnieniu, że stosunek dynamicznego współczynnika lepkości )i do gęstości cieczy p określany jest mianem kinematycznego współczynnika lepkości v:

I

V = •

(15.29)

otrzymuje się liczbę Reynoldsa wyrażoną w postaci:

LV Lv

—T=—=Re    (15.30)

v v

Równość liczb Reynoldsa na modelu i w naturze stanowi gwarancję prawidłowego wymodelowania sił tarcia.

W celu wyprowadzenia związków skal wybranych wielkości fizycznych porównano wyrażenie określające skale sił bezwładności (15.10) ze skalą siły tarcia (15.27):

a;

a;

.4

(15.31)

^aP~t^=aA^av=^au ■ a, *    “ et,

i otrzymano zależność określającą skalę czasu:

(15.32)

M 2 2-1

a. =—-a, =a;a_v

I

Związek ten pozwala na wyznaczenie skal innych wielkości fizycznych w funkcji skali długości a_L:

skala prędkości:	a, &,av _i av = —^=-V- = c^a,^1a, al	(15.33)
skala przepływu:	aQ = avaA = avaA aj = avaŁ	(15.34)
skala siły*.	% -a^a, =avapaAava^ = apa$	(15.35)
skala ciśnienia:	_ olf _ apa; ^P~ *A~ OL^2l	(15.36)