Image14 (37)

32 Rozwiązania zadań ze zbioru "MENDLA

Napiszemy równanie Clapeyrona dla naczynia pierwszego:

p-i • V = — • R • T /: V Pi

rm • R • T

stąd pi =

pi • V

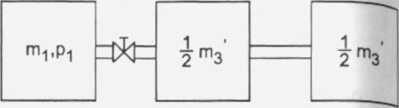
Nieznane wielkości m, p, T, V znajdujemy z innych zależności.

Po zamknięciu zaworu drugiego i otwarciu zaworu pierwszego ciśnienia w obu naczyniach wyrównają się osiągając jednakową wartość p.

Objętość obu naczyń wynosi V_c = 2 • V, a całkowita masa gazu m będzie:

1    2 • rm + m3

m = mi + - • m3 =-^-

Z równania Clapeyrona dla obu naczyń (I i II) otrzymamy:

p • V_c = — • R • T P

p ■ V_c • p = m • R • T m ■ R T ^M “ p • V_c

/•p

/: p • V_c

Za m i V_c podstawiamy do p odpowiednie wzory. 2 • rm + nri3

R • T

Stąd p =

p • 2 • V (2 • rm + m3)- R • T 4 • p • V

Po podstawieniu do równania na ciśnienie pi otrzymamy: rm • R ■ T

^P1 (2 • rm + m₃> R • T 4 • p • V

V

pi = rm P1 =

⁴P

2 • rm + m3

4 - rm • p

2 • nm + rri3

Jednostki:

_ 4 • 0,003 • 250000 ^P1 2 • 0,003 + 0,004

²⁵⁰⁰⁰⁰

_______Rozwiązania zadań ze zbioru "MF.NDLA "_

pi = 300000 Pa pi = 300 kPa

Odp.: Ciśnienie początkowe w pierwszym naczyniu wynosiło 300 kPa.

Zadanie 559 str.111

Dane:

V = 682 dm³ = 0,682 m³ mi = 12g= 0,012/cg

ti = 20°C

rri2 = 18p= 0,018kg

t₂ = i oo °c

Szukane:

Pi = ?

P2 = ?

n = 28-^—. = 0,028 ^r mol

Jkg_

mol

R = 8,31

J

mol • K

Sytuacja początkowa

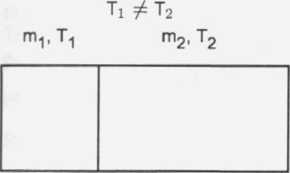
Sytuacja po wyrównaniu temperatur

Ti = T₂ = T

m₁,p₁,T    m₂, p₂, T

Korzystając z równania bilansu cieplnego otrzymamy:

Qp = Qo - energia cieplna Q_p pobrana przez azot znajdujący się w naczyniu pierwszym jest równa energii oddanej Q₀ przez azot z naczynia drugiego.

Q_p = mi • c • (T - Ti) oraz Q₀ = m₂ • c • (T₂ - T)

gdzie Ti = ti + 273K\    T2 = t2 + 273/<

Po podstawieniu do równania bilansu cieplnego otrzymamy: mi • c- (T - Ti) = 1712 • c • (T2 - T) /: c mi • (T - Ti) = rri2 • (T2 - T)

Po dalszych przekształceniach obliczymy temperaturę T jednakową dla obu części naczynia.

rm • T - rm • Ti = rri2 • T2 - m2 • T rm • T + rri2 • T = rm • Ti + rri2 • T2 T • (rm + rri2) = mi • Ti + m2 • T2 /: (mi + m2)

3 —Zeszyt 5