image136

70

4. Badanie podstawowych właściwości mechanicznych

gdzie: F - maksymalna siła odkształcająca, N; A₀ - powierzchnia początkowego przekroju poprzecznego odcinka pomiarowego, m², cm², mm².

Wytrzymałość na rozciąganie jest więc maksymalnym naprężeniem jakie, materiał przenosi podczas krótkotrwałego rozciągania statycznego.

Obliczanie pola przekroju poprzecznego. Pole przekroju poprzecznego A₍₎ próbek wiosełkowych wg normy [2] o prostopadłościennym odcinku pomiarowym określa wzór

(4.8)

gdzie: g - grubość odcinka pomiarowego, m, cm, mm; b - szerokość odcinka pomiarowego, m, cm, mm.

Pomiary wykonuje się mikrometrem zapewniającym dokładność do 0,01 mm i wywierającego na próbkę ciśnienie nie większe od 0,03 MPa.

Gdy zachodzi potrzeba znalezienia rzeczywistego naprężenia, jakie występuje w mocno przewężonej próbce w momencie zerwania, można do obliczenia powierzchni zastosować wzór (4.5).

Inaczej określa się wytrzymałość na rozciąganie tkanin powlekanych tworzywami sztucznymi. Przez wytrzymałość na rozciąganie należy tu rozumieć siłę potrzebną do rozerwania próbki bez odnoszenia jej do przekroju poprzecznego. Jest to więc w istocie siła niszcząca.

Wydłużenia względne przy zerwaniu ą (także w odniesieniu do tkanin powlekanych) wyraża się wzorem (4.2) lub (4.3).

Prędkość rozciągania wpływa w znaczący sposób na wynik pomiaru. Należy dobierać ją w zależności od rodzaju tworzywa zgodnie z normami [2]-[6]. Mogą one wynosić od 1 mm/min dla sztywnych tworzyw konstrukcyjnych do 500 mm/min dla folii elastycznych.

Wyznaczanie modułu sprężystości wzdłużnej podczas rozciągania. Moduł sprężystości wzdłużnej E wynika z zależności wyrażonej wzorem (4.6a), po przekształceniu którego

E = —, MPa    (4.9)

£

Jest to więc stosunek naprężenia do odpowiadającego mu wydłużenia względnego, ale w zakresie prostoliniowego przebiegu wykresu rozciągania (rys. 4.6--4.9). W zastosowaniach praktycznych wzór przybiera postać

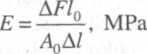
(4.10)

4.2. Badanie cech wytrzymałościowych podczas rozciągania

71

gdzie: E - moduł sprężystości wzdłużnej Younga, MPa; AF - przyrost obciążenia, N; Al - przyrost odkształcenia bezwzględnego, m, cm, mm; A₀- początko-wy przekrój poprzeczny odcinka pomiarowego, m", mm".

Moduł sprężystości wzdłużnej można rozważać jako tangens kąta, pod którym jest nachylony prostoliniowy odcinek wykresu rozciągania względem osi rozciągania. Na rysunku 4.7 widać, że dla miękkiego plastyfikatu PVC wyznaczanie modułu sprężystości nie ma sensu, chociaż spotyka się przybliżone dane na ten temat, np.

1)    moduł sprężystości polietylenu, a więc tworzywa miękkiego, ocenia się na 130 MPa;

2)    moduł sprężystości poli(metakrylanu metylu) i polistyrenu, a więc tworzyw podatnych na odkształcenia, ale już mających właściwości konstrukcyjne, wynosi 2500-3500 MPa;

3)    typowe tworzywa konstrukcyjne, laminaty poliestrowo- lub epoksydo-wo-szklane osiągają moduły 35 000-50 000 MPa;

4)    konwencjonalne stale mają moduł Younga 210 000 MPa.

Poglądowe porównanie tych materiałów przedstawiono na rys. 4.3.

Skomputeryzowane, nowoczesne maszyny wytrzymałościowe (aparaty do badania właściwości mechanicznych tworzyw sztucznych) mają zaprogramowane wyznaczanie modułu sprężystości, tzn. obliczają go na podstawie początkowego przebiegu krzywej rozciągania i wyniki podają w postaci tabel. Jak widać wyraźnie z rys. 4.6, dla polistyrenu udaje się to łatwo, dla ABS i poliamidu udaje się wówczas, gdy odkształcenie nie przekroczy pewnego zakresu (rys. 4.8 i 4.9), a w ogóle nie uda się w przypadku folii ze splastyfikowanego polichlorku winylu). Dlatego oznaczanie modułu sprężystości wg PN-82/C--89051, jakkolwiek poprawne, wydaje się mało przydatne w praktyce.

Wyznaczanie naprężeń odpowiadających określonym wydłużeniom względnym. W odniesieniu do łatwo odkształcalnych tworzyw moduł E ma znaczenie raczej teoretyczne. Rzeczywiste naprężenia odpowiadające odkształceniom mogącym pojawić się w czasie eksploatacji znacznie odbiegają od tych, których można by oczekiwać na podstawie modułu sprężystości. Dlatego też charakteryzując takie tworzywa, rezygnuje się najczęściej z podawania modułu E, a wprowadza naprężenia odpowiadające wyróżnionym wartościom wydłużenia względnego. Naprężenia te bywają nazywane modułami przy określonych wydłużeniach względnych; mówi się np. o module przy 100% wydłużenia (rys. 4.11). Naprężenia te są łatwiejsze do zmierzenia. Na rysunku 4.7 zaznaczono jak graficznie znajduje się moduł przy 100% odkształcenia, wiedząc, że badana próbka miała odcinek pomiarowy długości 100 mm.