image108

98

4. Badanie podstawowych właściwości mechanicznych

stąd

b =

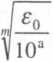
(4.28)

W celu znalezienia parametrów tego równania, (tj. a oraz tri) najdogodniej jest posłużyć się metodą najmniejszych kwadratów. Układ równań normalnych przedstawia się następująco:

n    n

an + mJ'_jx =

i=l    /=!

x + m

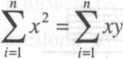
(4.29)

Poniżej zestawiono wyniki sześciu pomiarów pełzania plastobetonu pod naprężeniem 4,75 MPa i wyniki potrzebnych obliczeń, a u dołu kolumn sumy do równań (4.29). Natychmiastowe odkształcenie fb wyniosło 2,32-KT*

Czas obciążenia, h	£1	x = lgt	y = lg£i	x^2	*y
0,5	2,53	-0,3010	0,4031	0,0906	0,1213
1,0	2,63	0,0	0,4200	0,0	0,0
2,0	2,72	0,3010	0,4346	0,0906	0,1308
50,0	3,84	1,6990	0,5843	2,8866	0,9927
71,5	4,85	1,8543	0,6857	3,4384	1,2715
120,5	5,75	2,0882	0,7597	4,3606	1,5864
Suma Z		5,6415	3,2874	10,8668	4,1027

Rozwiązanie układu równań (4.29) prowadzi do znalezienia stałych m = 0,13839 oraz b = 0,41790, oczywiście obowiązujących dla naprężenia 4,75 MPa lub zbliżonych, charakteryzujących pełzanie tego plastobetonu.

Ocena wyników pomiarów pełzania. Równanie Mac Leoda można wykorzystywać następująco:

1)    wstawiając dowolny czas t do równania (4.25) można obliczyć odkształcenie, którego zmierzenie wymagałoby pomiaru trwającego zbyt długo;

2)    można obliczyć czas, po którym plastobeton lub ogólnie tworzywo osiągnie jakieś założone odkształcenie, np. połowę odkształcenia, niszczące próbkę. W tym celu należy równanie przekształcić do postaci

t = b

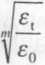
(4.30)

4.6. Badania długotrwale - pełzanie, wytrzymałość długotrwała

99

i wstawić do niego nie £_ma._v, ale jego połowę. Krytyczne £_max, które należy zmierzyć w próbie krótkotrwałej dla danego plastobetonu, wynosi 3,6-10'³; wtedy bezpieczne odkształcenie wyniesie 1,8-10^-3. Obliczony czas, po którym plas-tobeton osiągnie w wyniku pełzania to bezpieczne odkształcenie, wyniesie 1 128 296 h, co równa się 128 lat. Z równania (4.30) można teoretycznie obliczyć, że krzywa pełzania przetnie się z maksymalnym odkształceniem, tj. 3,6-1CT³, po 386 min lat. Ten czysto teoretyczny wynik zakłada, że panować będą stale te same warunki naprężenia, temperatury i wilgotności.

4.7. Twardość tworzyw sztucznych

Pojęcie twardości w odniesieniu do tworzyw sztucznych określa się za pomocą oporu, jaki stawia materiał, gdy wciska się w jego powierzchnię pionowo odpowiedni wgłębnik, stosując naciski tak wielkie, aby powstało odkształcenie trwałe. Jako wgłębniki stosuje się tu elementy o znormalizowanych kształtach, np. kulki, stożki lub piramidki.

4.7.1. Zasady oznaczania twardości

Metoda wciskania kulki [23]. Metoda polega na powolnym wciskaniu stalowej kulki w badane tworzywo (rys. 4.32). Po upływie pewnego czasu ustala się stan równowagi, w którym zwiększająca się powierzchnia odcisku równoważy wywierane obciążenie przez wgłębiającą się kulkę. W tym stanie stosunek siły obciążającej do powierzchni odcisku wgniecionego w badanym materiale określa jego twardość

H =_2bciy=ra=-₌ £_nW    (4.31)

powierzchnia odcisku A

gdzie: F, - zastosowane obciążenie, N; A - powierzchnia odcisku, mm².

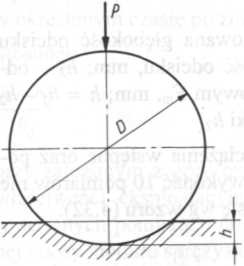
Rys. 4.32. Geometryczne dane do obliczania twardości metodą wciskania kulki

P - kierunek nacisku, D - średnica kulki, h - głębokość wgniotu