Image37

72

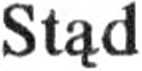
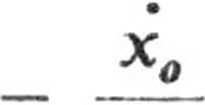
2 m

= — sińcom

CD

W polu sił Hooke’a ciało drga sinusoidalnie wokół położenia równowagi Okres tych drgań znajdziemy z warunku

coT

b. O oscylatorze harmonicznym tłumionym mówimy wówczas, gdy oprócz siły typu Hooke’a = — kx istnieje siła F₂ tłumiąca ruch. Na ogół zakłada się, że siła tłumiąca jest proporcjonalna do prędkości lub kwadratu prędkości i skierowana przeciwnie do kierunku ruchu.

Rozpatrzmy ruch jednowymiarowy w ośrodku lepkim, gdzie F₂ = —bx (b - stała dodatnia). Równanie Newtona przyjmuje wtedy postać

x + 2<t x + a)²x = 0,

gdzie dokonano standardowych podstawień

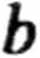
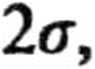
Jest to równanie różniczkowe drugiego rzędu, liniowe jednorodne. Rozwiązując je, podobnie jak równanie oscylatora harmonicznego nietłumionego, mamy

X = e~ⁿ (C_Ł esl*¹-*'' + c₂ e-V»²-“²‘).

Przyjmując warunki początkowe

dostaje]

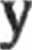
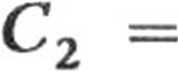
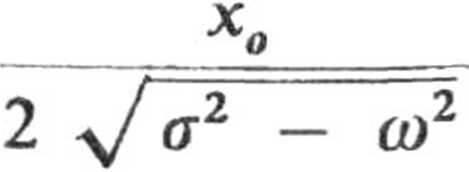
Rozwiązanie ogólne równania ruchu przybiera więc postać

_v cr2 — cjl j

2

— yj a² — (o² t

lub inaczej

Zauważmy, że w zależności od tego

0 (tzw.

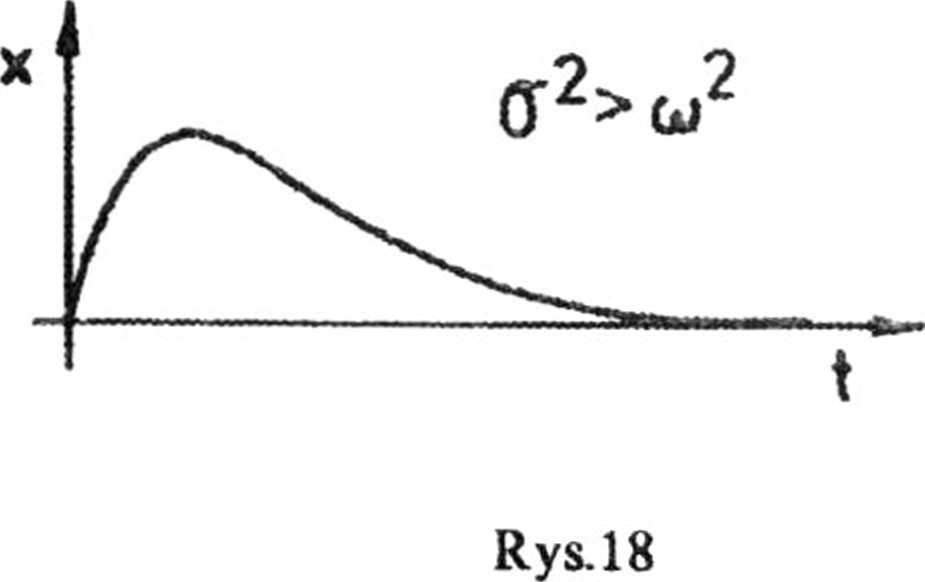
aperiodyczny), czy o² — w²

yfa² — co² przybiera odpowiednio wartość rzeczywistą lub urojoną. W pierwszym przypadku, odpowiadającemu dużemu oporowi ośrodka, następuje tylko jednorazowe wychylenie z położenia równowagi (rys. 18). Ruch taki nazywamy pełzającym.

Przy małej lepkości ośrodka, tzn. gdy

o² < co²

czy a* — przypadek

co² > 0 (tzw. przypadek periodyczny), pierwiastek

yj o² — [O²    = i y[a)² — O² .

Wtedy rozwiązanie równania ruchu można przepisać jeszcze raz w formie

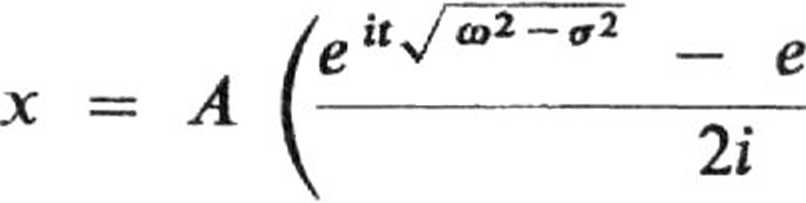
gdzie:

A =

przedstawia malejącą wykładniczo amplitudę ruchu (rys. 19).