Image80 (7)

158

P(B) — P (A_t w A₂ u A₃) = P(A_t) + P(A₂) + P(X₃) - P(A_l n A₂) -- PUj n /l₃) - P(A₂ n X₃) + P(A_t n A₂ n A₃) = P(A₃) + P(A₂) + + PU₃) - P(AJ ■ P(A₂) - P(AJ ■ P(A₃) - P(A₂) ■ P(A₃) 4-+ P(A_t) ■ P(A₂)■ P(A₃) = 0,64.

5.14

a. Prawdopodobieństwo trafienia się w trakcie pierwszej próby wynosi

q — więc prawodopodobieństwo pozostania przy życiu po pierwszej kolejce 6

wynosi

b. Aby przeżyć w n-tej kolejce należy odnosić same sukcesy. Ze schematu Bernoulliego obliczymy prawdopodobieństwo n sukcesów w n próbach

5.15

a

mamy:

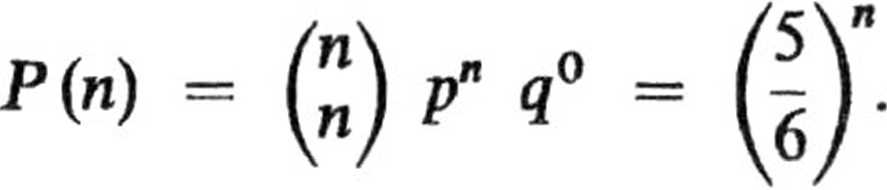
. Zakładając, że dalsze rzuty dałyby taki sam rozkład wyrzuconych liczb,

P(6) =

3000

1000 + 2000 + 3000

1

3

b. Wagę statystyczną poszczególnych zdarzeń można zdefiniować jako liczbę określającą ile razy prawdopodobieństwo tych zdarzeń jest większe od prawdopodobieństwa jednego (dowolnego) z możliwych wydarzeń. Nie jest więc ona na ogół jednoznacznie określona. Często odnosimy ją do stanu najmniej prawdopodobnego. Odnieśmy ją więc do prawdopodobieństwa wyrzucenia 1. Wtedy wagi statyczne wynoszą:

0(1)

0(2) = 0(3) = 0(4) = 1,

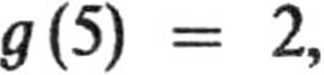
0(6) = 3.

c. P{k)

gih)

Z e(ⁿY

5.16

a. Podać stan mikro, to znaczy szczegółowe rozmieszczenie każdej z 3 cząstek z osobna. Na przykład:

cząstka    nr    1    znajduje    się    w    stanie    a,

cząstka    nr    2    znajduje    się    w    stanie    a,

cząstka    nr    3    znajduje    się    w    stanie    b.

Podać stan makro, to znaczy liczbowe rozmieszczenie cząstek po poszczególnych możliwych stanach. Na przykład w stanie a znajdują się 2 cząstki, w stanie b zaś 1 cząstka.

b. Stan makro (2 cząstki w stanie a, 1 cząstka w stanie b) może być zrealizowany na następujące sposoby:

cząstka    nr    1    i    2    w    stanie    a,    cząstka    nr    3    w    stanie    b,

cząstka    nr    1    i    3    w    stanie    a,    cząstka    nr    2    w    stanie    b_y

cząstka    nr    2    i    3    w    stanie    a,    cząstka    nr    1    w    stanie    b.

Stąd

P = 3 P_Q.

Stan makro: 3 cząstki w stanie a może być zrealizowany na jeden sposób. Zate, dla tego stanu makro

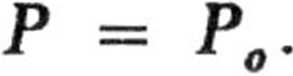
c. Oznaczmy przez P(n_a) prawdopodobieństwo takiego stanu makro, że w stanie a są n_a cząstki. Wówczas w stanie b znajduje się 3 — n_a = n_b cząstek. Mamy wtedy

P(Qa)

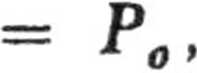
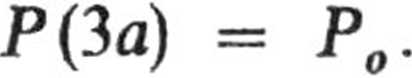
P. znajdujemy z warunku normalizacji

8 P₀ = 1,

tj-

P₀ = 1/8.