img053 (31)

53

lub

^dr =

2 L sin² ^

(33)

natomiast gdy posiadamy z niwelacji różnicę wysokości Ah, to wychodząc z twierdzenia Pitagorasa, otrzymuje się zależność, która po rozwinięciu w szereg daje wzór (24)

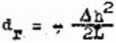
(34)

W praktycznym użyciu najchętniej stosuje się wzór (22), jako dający bezpośrednio długość zredukowaną, lub wzór (24).

21ie wszystkie przedstawi one wzory ca poprawki muszą być stosowane ćo każdego uwaiaru. Przeprowadzając ich analizę można ustalić, dla jakich warunków i 7^daganych dokładności poszczęgólne poprawki mesą być zaniodbywa ln« przy ostatecznym obliczaniu długości poziomaj, o czym szerzej traktują podręczniki dla geodetów.

Formularz 1 przedstawia przykład układu formularza dla pomiarów długości w kopalni z obliczcnymi poprawkami.

2.2.2* Pośrednia pomiary dłu^cścl

Metody .bezpośrednie pomiarów długości są pracochłonno i kosztowne, zwłaszcza przy wymaganej wysokiej dokładności. Jeżeli mierzony odcinek prze:hodzi przez przeszkodę (rzekę, wąwóz itd.)‘ lub łączy punkty ułwćc-scępr.e, wówczas bezpośredni pomiar jest nawet niemożliwy. Dlatego też obok metod bezpośrednich rozwijały się w geodezji również metody pośrednie pomiarów długości, a najnowsze zastosowaniu dalmierzy elektromagnetycznych (elektronicznych) są pod każdym względom, wyrazem postępu uuuko-wo-toohnicznego i zapewniają wysoką dokładność pomiarów.

Pośrednie pomiary długości za pomocą d o n o 1 a y o h konstrukcji geometrycznych. Metoda ta połogu na obliczeniu długości niedostępnego odcina jako elet.idr.su trójkąta lub czworoboku, w. którym pomierzono bezpośrednio inno elementy pomocnicze długościowe lub długościowe i kątowe. i'o r*uj-bardziej typowych i rmjczęściej stosowanych przykładów należy rozwiązanie trójkąta, gdy jeden z końców mierzonego cćci nka jest niedostępny (tz-.7, wcięcie w przód), lub rozwiązanie czworoboku, Sóy oba kobee są niedostępne (tz"/c zagadnienie Kaunena).

a) Tjcięcio w przód (część zagadnieniu dotycząca wyznaczeniu ił :t;ośc.l). tfle trując możności zmierzenia odcinka niedostępnego źli, -mierzymy dok ładni o pomooniczy odcinek AC ~ b (baza) oraz kąty a i j- (ays. 3*3) ■ -hi puu-s tą. ile twierdzenia sinusów nożsmy na pi:, ć