img307 (5)

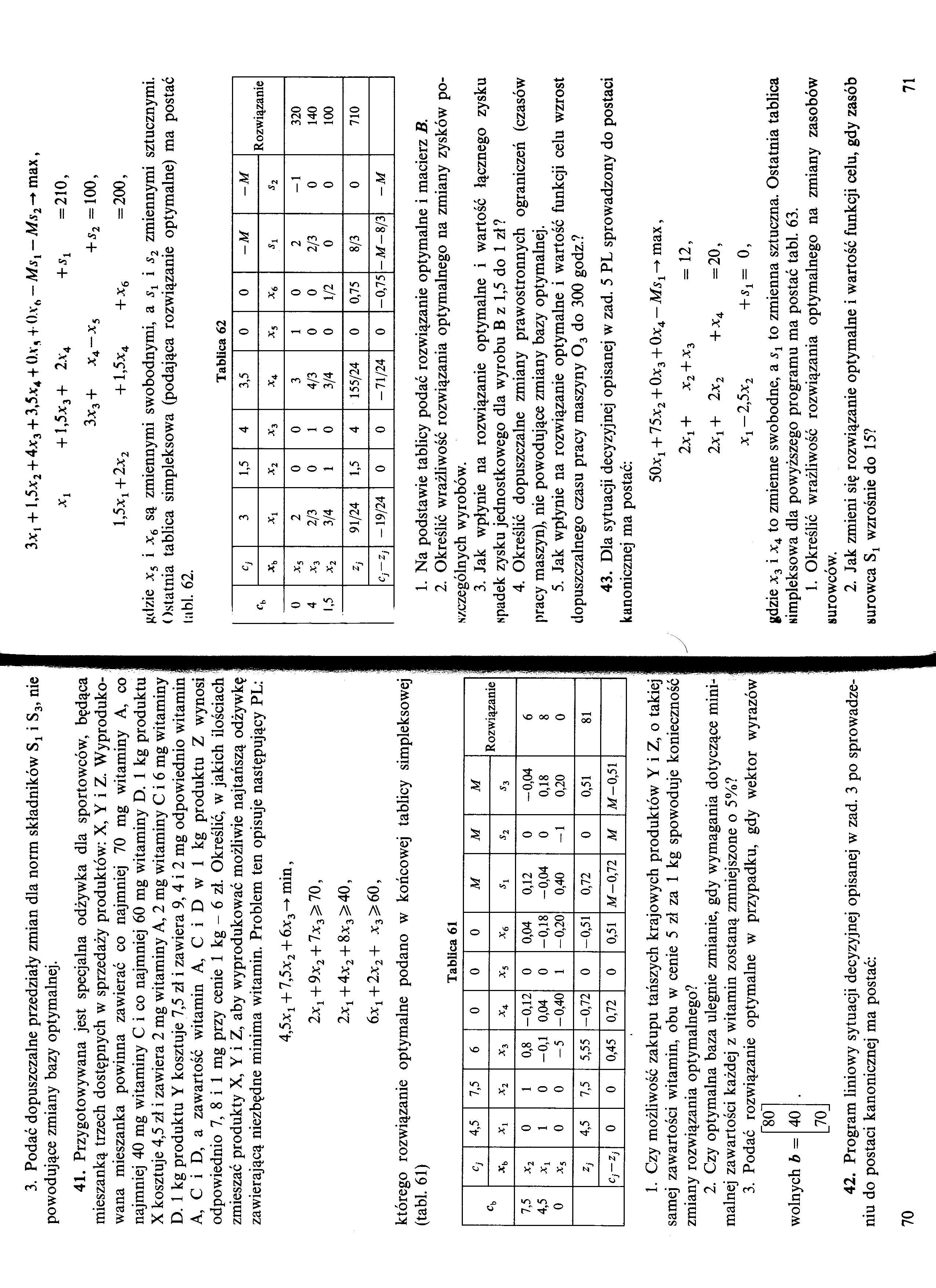
3. Podać dopuszczalne przedziały zmian dla norm składników S_x i S₃, nie powodujące zmiany bazy optymalnej.

41. Przygotowywana jest specjalna odżywka dla sportowców, będąca mieszanką trzech dostępnych w sprzedaży produktów: X, Y i Z. Wyprodukowana mieszanka powinna zawierać co najmniej 70 mg witaminy A, co najmniej 40 mg witaminy C i co najmniej 60 mg witaminy D. 1 kg produktu X kosztuje 4,5 zł i zawiera 2 mg witaminy A, 2 mg witaminy C i 6 mg witaminy ] D. 1 kg produktu Y kosztuje 7,5 zł i zawiera 9, 4 i 2 mg odpowiednio witamin j A, C i D, a zawartość witamin A, C i D w 1 kg produktu Z wynosi odpowiednio 7, 8 i 1 mg przy cenie 1 kg - 6 zł. Określić, w jakich ilościach | zmieszać produkty X, Y i Z, aby wyprodukować możliwie najtańszą odżywkę zawierającą niezbędne minima witamin. Problem ten opisuje następujący PL:

4,5x j + 7,5 x₂ + 6x₃ -*• min,

2x₁ + 9x₂ + 7x₃ ^ 70,

2x_t + 4x₂ + 8x₃ ^ 40,

6x₁+2x₂+ x₃>60,

którego rozwiązanie optymalne podano w końcowej tablicy simpleksowej ] (tabl. 61)

Tablica 61

	^C1	4,5	7,5	6	0	0	0	M	M	M	Rozwiązanie j
^Cb	*b	*1	*2	*3	*4	*5	*6		*2	Si
7,5	*2	0	1	0,8	-0,12	0	0,04	0,12	0	-0,04	6
4,5	*1	1	0	-0,1	0,04	0	1 © OO	-0,04	0	0,18	8
0	*5	0	0	-5	-0,40	1	-0,20	0,40	-1	0,20	0
	^zi	4,5	7,5	5,55	-0,72	0	-0,51	0,72	0	0,51	81 1
	^cJ~^zi	0	0	0,45	0,72	0	0,51	Af—0,72	M	M—0,51

1.    Czy możliwość zakupu tańszych krajowych produktów Y i Z, o takiej samej zawartości witamin, obu w cenie 5 zł za 1 kg spowoduje koniecznośc i zmiany rozwiązania optymalnego?

2.    Czy optymalna baza ulegnie zmianie, gdy wymagania dotyczące minimalnej zawartości każdej z witamin zostaną zmniejszone o 5%?

3.    Podać rozwiązanie optymalne w przypadku, gdy wektor wyrazów i 80

wolnych b

40

70

42. Program liniowy sytuacji decyzyjnej opisanej w zad. 3 po sprowadzeniu do postaci kanonicznej ma postać:

3*, + l,5*₂ + 4*₃ + 3,5*₄ + 0.v_l, + ()x_b-Ms_l—Ms_i-* max,

x_i +1,5*3+ 2*₄    + s_x =210,

3*3+ *4 —*5    + S₂=100,

1,5*3 + 2*₂    +1,5*4    + *5    =200,

Hilzie *₅ i *₆ są zmiennymi swobodnymi, a j, i s₂ zmiennymi sztucznymi. Ostatnia tablica simpleksowa (podająca rozwiązanie optymalne) ma postać lubi. 62.

Tablica 62

fb	^ci	3	1,5	4	3,5	0	0	-M	-M	Rozwiązanie
		x1	x2	*3	*4	*5	*6	+	*2
0	x5	2	0	0	3	1	0	2	-1	320
4	x3	2/3	0	1	4/3	0	0	2/3	0	140
1,5	X2	3/4	1	0	3/4	0	1/2	0	0	100
	^zi	91/24	1,5	4	155/24	0	0,75	8/3	0	710
	^CJ~^ZJ	-19/24	0	0	-71/24	0	-0,75	1 * 1 00	-M

1.    Na podstawie tablicy podać rozwiązanie optymalne i macierz B.

2.    Określić wrażliwość rozwiązania optymalnego na zmiany zysków poszczególnych wyrobów.

3.    Jak wpłynie na rozwiązanie optymalne i wartość łącznego zysku spadek zysku jednostkowego dla wyrobu B z 1,5 do 1 zł?

4.    Określić dopuszczalne zmiany prawostronnych ograniczeń (czasów pracy maszyn), nie powodujące zmiany bazy optymalnej.

5.    Jak wpłynie na rozwiązanie optymalne i wartość funkcji celu wzrost dopuszczalnego czasu pracy maszyny 0₃ do 300 godz.?

43. Dla sytuacji decyzyjnej opisanej w zad. 5 PL sprowadzony do postaci kanonicznej ma postać:

50*j + 75*2 + 0*3 + 0*4 — Ms_x -> max,

2*j +    *₂ +*3    =12,

2*!+    2*2    + *4    =20,

x₁ — 2,5*₂    + s_x =

gdzie *₃ i *4 to zmienne swobodne, a s₁ to zmienna sztuczna. Ostatnia tablica simpleksowa dla powyższego programu ma postać tabl. 63.

1.    Określić wrażliwość rozwiązania optymalnego na zmiany zasobów surowców.

2.    Jak zmieni się rozwiązanie optymalne i wartość funkcji celu, gdy zasób surowca S_x wzrośnie do 15?

71