Untitled Scanned 44 (3)

Zgodnie z zasadami podanymi w p. 13.2 określono wartości T i N oraz sporządzono ich wykresy (rys. 13.43g, h). Analiza powyższych wykresów pozwala na stwierdzenie spełnienia przez rozwiązanie warunków równowagi.

Zgodność przemieszczeń sprawdzimy obliczając poziome przesunięcia punktów A i E układu rzeczywistego. W tym celu obciążamy układ podstawowy raz siłą P_A = 1 w punkcie A i drugi raz siłą P_E=1 w punkcie E wzdłuż kierunku poziomego. Otrzymane wykresy momentów (rys. 13.43i, j) wykorzystujemy stosując wzór (13.9).

Przesunięcie poziome punktu E=A_Ea;

^    i    2    t

—    =---3,0- 0,05553 • — 3,0---3,0(0,12300+

a    2    3    2

1 2

- 0,01986)- 3,0( - —• 3,0 • 0,12300-—■ 3,0) +1 = - 0,99972 +1 = 0,00028;

0,00028

błąd wynosi _{0 99972} * ¹⁰°—°»°³%

Przesunięcie poziome punktu A = A_Aa;

—    = — • 3,0 ( - 0,06747 • — • 3,0 - 0,06747 • 3,0+0,07539 • 3,0+

a 2    3

+ 0,05553 • —• 3,0)^ — (0,33723 - 0,33735) = -—• 0,00012 ;

3    2    2

0,00012

błąd wynosi -    • 100 =0,04%

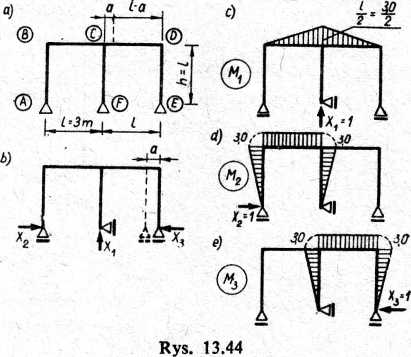
Przykład 13.8. Rozwiązać ramę z przykładu 13.7 (rys. 13.44a) przyjmując inny układ podstawowy. Odrzucimy również trzy więzy względnie niezbędne lecz tak, aby żaden z nich nie pokrywał się z brakującym odcinkiem rygla "CD (rys. 13.44b).

Zgodnie ze wzorem (13.35) zapiszemy:

Sn Xi + 6u Xz+Si3 X3+A_t,=0;

S2I Xi + S2I Xz +    X$ + ^2o ”0 j    (A)

&31 Xl+Ó32 X2 + Ó33 X3 + A3„ = 0 .

1

Wartości przemieszczeń na skutek skrócenia rygla CD wynoszą:

Ai_a=0;    A 2«=0;    A₃„— — ^ 7?3^= — ( — 1 • a)=a.

482