IMGW97 (3)

Rozdział 5

Widmo elektronowe

Elektrony w molekule poruszają się wokół jąder, mają więc pewną energię I kinetyczną. Ponieważ znajdują się one w polu sił elektrostatycznych przyciągania | przez jądra i odpychania przez sąsiadujące elektrony, mają więc również energię | potencjalną. W odróżnieniu od rotacji, których modelem mechanicznym jest | wirujący bąk, lub oscylacji, których modelem jest drganie kulek połączonych [; sprężynami, ruch elektronów trudno jest rozważać na przykładzie jakiegoś modelu g mechanicznego. Nie przyporządkowuje się też elektronom stopni swobody, gdyż l byłoby to zbyt skomplikowane, a poza tym mało użyteczne.

5.1. Charakterystyka stanów elektronowych

W modelu Bohra elektron jest kulką o masie m_e = 9,1094-10"³¹ kg i eleraen- j tarnym ładunku elektrycznym e = —1,6022 -10"¹⁹ C. Kulka krąży wokół jądra po I orbicie o ustalonych parametrach, które mogą się zmieniać tylko skokowo, kiedy 1 elektron przeskakuje na inną orbitę. Orbitom przypisujemy kolejne główne liczby | kwantowe n = 1,2, 3, ...

W modelu Bohra, opisującym atom wodoru lub atom wodoropodobny, elektron | jest potraktowany zbyt schematycznie, gdy spojrzymy na to z punktu widzenia | mechaniki kwantowej. W mechanice kwantowej traktuje się elektrony jako chmurę 1 prawdopodobieństwa znalezienia ładunku elektronowego w przestrzeni wokół jądn. I Jednak ruch tak określonych elektronów wykazuje cechy kojarzące się z ruchem | kulki po orbicie, a mianowicie ma realny, mierzalny doświadczalnie, moment pędu § orbitalnego. Moment pędu elektronu jest skwantowany i jego wartość wynosi i y/l(l + 1)A, gdzie orbitalna liczba kwantowa / może przybierać wartość \ 0,1,2,.... n — 1. Na orbicie o głównej liczbie kwantowej n *= 1 orbitalna liczba | kwantowa l — 0; gdy n — 2, l może przybierać wartości 0 lub 1; gdy n = 3, l = 0,1,2; I gdy ««* 4, / =* 0,1,2,3 itd. Zamiast oznaczania cyframi orbitalnych liczb kwan- f towych l wprowadzono następującą symbolikę literową:

/■*01 23 4 orbita! atomowy s p d f g Rozróżniamy więc w atomie orbitale s, p, d, /, g.

Pod wpływem pola elektrycznego lub magnetycznego następuje precesja wektora momentu pędu wokół kierunku działającego pola przedstawiona na rys. 5.1. Kąt a między wektorem momentu pędu a kierunkiem pola jest skwantowany w taki sposób, że rzut orbitalnego momentu pędu Jl(l + l)fi na kierunek pola wynosi mfi, przy czym m, jest magnetyczną liczbą kwantową, która może przybierać wartości ni, =    — 1), (/ — 2),.... 0,(—1 4- 2), (—/ + 1), — Pod wpływem działającego nań

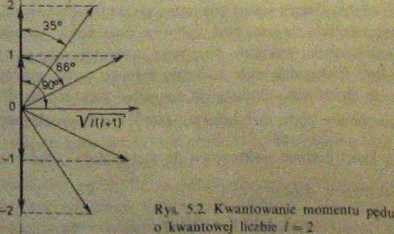
pola wektor momentu pędu o kwantowej liczbie 1 może przybierać 21 + 1 różnych orientacji względem kierunku pola, wykonując precesję pod odpowiednim kątem (rys. 5.2). Każda z wyróżnionych orientacji ma określoną energię oddziaływania wektora momentu pędu z polem i wskutek skwantowania orientacji energie ich są również skwantowane. Oczywiście, jeśli na układ nie działa żadne pole, to orientacje wektora momentu pędu są dowolne i bezładne, a odpowiadające im stany mają jednakową energię, czyli są (21+ l)-krotnie zdegenerowane. Warto zwrócić uwagę, że nie tylko moment orbitalny, ale każdy moment pędu ulega opisanemu kwantowaniu. Przypomnijmy, że opisane w punkcie 2.1 rotacyjne poziomy energetyczne o kwantowej liczbie rotacji J są (2J + lj-krotnie zdegenerowane.

kierunek pola '

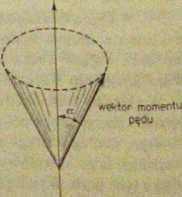
Rys, 5.1 Precesja wektora momentu pędu wokół osi kierunku pola elektrycznego lub magnetycznego

' 1 kierunek peta

illl "U -