IMG�76 (2)

wskazaniu pozostanie laki, jaki jest. Na podstawie znajomości konstrukcji miernika możemy jednak wiedzieć, do jakiego zbioru mierników powinien należeć nasz egzemplarz miernika i jaki może być rozkład prawdopodobieństwa błędów różnych wskazań różnych egzemplarzy mierników tego typu, a nasze wskazanie jest losowa realizacja wskazania jednego z nich Takie dane mogą być solidną daną probabilistyczną o rozkładzie błędów wskazań jako podstawy oceny niepewności, a konkretnie w danym przypadku składowej niepewności typu B Gdyby szczegółowe dane były niedostępne, moZemy przyjąć najbardziej niekorzystny ale uzasadniony rozkład gęstości prawdopodobieństwa błędów wskazań, bo w ten sposób otrzymamy nasze oszacowania niepewności i tak lepsze, niż gdybyśmy nie korzystali z takiego postępowania

Przedstawione rozważania powinny więc przekonać, że stosowanie probabilistycznych modeli do analizy skutków występowania błędów zarówno tych, które prowadzą do niepewności typu A, jak i tych, które prowadzą do niepewności typu B, jest racjonalnym i pożytecznym rozwiązaniem zagadnienia oceny niepewności końcowego wyniku pomiaru.

Rozpatrzymy (spekulatywnie) proces powstawania błędów losowych, których skutkiem jest niepewność typu A

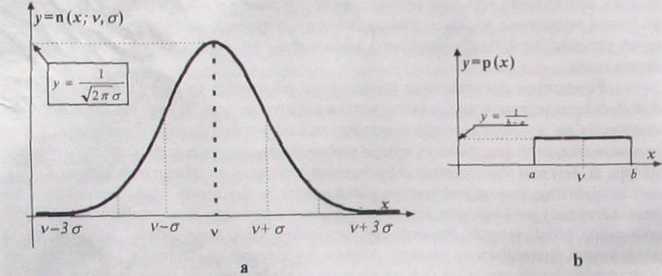
Rys. 1.1. Krzywe funkcji rozkładu: a - normalnego, b - jednostajnego (równomiernego)

1

P⁽*)“-7r=-^e

v2zrtr

= n(x,v,a)

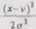
(18)

Zakładając, że losowość wyników pomiaru, poprzez którą ujawnia się losowość błędów, jest z zasady wypadkowym skutkiem wielu przyczyn, często niezależnych, to musimy przyjąć, że obserwowane błędy są wypadkowymi błędami powstałymi z sumowania się składowych spowodowanych przez właściwe im przyczyny Gdy więc obserwowane skutki są sumą losowych składników, to ich wypadkowy rozkład jest kompozycją (złożeniem, splotem) rozkładów opisujących losowość składników. Na podstawie teorii rachunku prawdopodobieństwa możemy więc oczekiwać, że tę wypadkową losowość będzie dobrze opisywać normalny rozkład gęstości prawdopodobieństwa, którego funkcją jest funkcja Gaussa (1.8, rys la)¹. Nawet tam, gdzie rozkład normalny nie jest dokładnym modelem

rozkładu danych doświadczalnych, stosujemy go jako przybliżenie, ponieważ jest często używany, dobrze znany i dostępny w kalkulatorach lub w innych technicznych pomocach obliczeniowych (a jest wystarczająco dokładny).

Funkcja gęstości prawdopodobieństwa zmiennej X (18) rozkładu normalnego jest całkowicie określona, gdy znane są wartości parametrów vi a. Jak wiemy z probabilistyki v nazywa się wartością oczekiwaną zmiennej losowej X i przedstawia wartość współrzędnej środka ciężkości rozkładu. Inaczej wyrażając powiemy, że v przedstawia tę wartość zmiennej losowej, wokół której rozrzucone są losowo wszystkie jej możliwe wartości, natomiast parametr o jest odchyleniem standardowym (inaczej odchyleniem średniokwadrato-wym) tej zmiennej i jest liczbową miarą rozrzutu możliwych wartości zmiennej losowej. Im większe cr, tym bardziej są rozrzucone wartości zmiennej losowej wokół wartości oczekiwanej v, a gęstość prawdopodobieństwa (czyli rzędne y) dla wszystkich x są odpowiednio mniejsze.

W rachunku prawdopodobieństwa wymienione parametry v i cr są powszechnie używanymi parametrami do charakteryzowania podstawowych właściwości dowolnych zmiennych losowych (a więc nie tylko o rozkładzie normalnym). Gdy mamy parametry (vi o) zmiennych losowych (od których dodatkowo wymaga się niezależności), to do rozwiązania wielu ważnych zadań mamy wystarczające dane o zmiennej losowej i nie potrzebujemy znać funkcji gęstości prawdopodobieństwa. Na przykład znając wartości oczekiwane i odchylenia standardowe każdej ze zmiennych możemy prosto i dość dokładnie obliczyć wartość oczekiwaną i odchylenie standardowe dowolnej funkcji określonej na tych zmiennych losowych (oczywiście zmienne wyjściowe mogą być zmiennymi o dowolnych rozkładach).

O wyrażeniu występującym w wykładniku funkcji (1.8) mówi się, że jest o

unormowanym (standaryzowanym) odchyleniem wartości x zmiennej losowej od wartości oczekiwanej v. Operacja normowania jest taka sama dla zmiennych o dowolnym rozkładzie, nie tylko o rozkładzie normalnym. Do celów pomiarowych v interpretujemy jako nie znaną i poszukiwaną ewentualną wartość prawdziwą wyniku pomiaru wyrażoną we właściwych jej jednostkach, a w takim razie różnica przedstawia błąd bezwzględny danego (np. surowego) wyniku x. Dzieląc różnicę przez cr (wyrażone w tych samych fizycznych jednostkach) otrzymujemy bezwymiarowe przedstawienie błędu (bezwymiarowe, bo nie w jednostkach fizycznych) Bezwymiarowość ta faktycznie oznacza, że wyraziliśmy odchylenie * od v „w sigmach", czyli uczyniliśmy jednostką cr. Unormowanie zmiennej X umożliwia korzystanie z uniwersalnej postaci, np. funkcji (1.8) i wykonywanie obliczeń przy użyciu kalkulatorów lub tablic zawierających odpowiednie funkcje, bo w tych pomocach obliczeniowych zmienne losowe są prezentowane tylko w postaci unormowanej.

Tam gdzie możemy przypuszczać, że rozkład normalny byłby modelem zbyt optymistycznym (tzn nie ma np. podstaw zakładać, że odchylenia duże są mniej prawdopodobne). często korzysta się w analizie dokładności wyników pomiaru z rozkładu gęstości prawdopodobieństwa jednostajnego (równomiernego, prostokątnego). Jest to również rozkład symetryczny (rys Ib) o wartości oczekiwanej v = °i o odchyleniu standardowym

a = Łza Na przykład dla błędów zaokrąglania (kwantowania) z założenia przyjmuje się 2vJ

rozkład jednostajny, bo uważa się, że żadna z liczb, którą moglibyśmy otrzymać jako wynik

37

1

W probabilistyce udowadnia się, że rozkład normalny jest granicznym, wypadkowym rozkładem kompozycji rozkładów, gdy liczba składników (komponentów) dąży do nieskończoności. Praktycznie wystarczy zbudować kompozycję kilku rozkładów, żeby rozkład wypadkowy był „prawie normalny". Np. kompozycja trzykrotna rozkładów jednostajnych o tych samych parametrach jest krzywą złożoną z parabol, ale „wzrokowo" jest prawie nieodróżnialna od krzywej normalnej. Dla czterokrotnej kompozycji podobieństwo jest jeszcze większe. Wykres kompozycji rozkładu normalnego o danym v i <r i jednostajnego o takich samych parametrach jest nieodróżnialny „wzrokowo" od wykresu „czystej” funkcji rozkładu normalnego. W

każdym z przykładów mona jest o kształcie krzywej, bo wypadkowe paramcliy kompozycji będą zawsze i ściśle złożeniem parametrów rozkładów wyjściowych.