IMG�79 (2)

wościowego w ftjnkcji częstotliwości, ■ więc składową błędu wywołanej zmianą częstotliwości Jest oczywiste, ze z założenia ta składowa ma wartość zero dla )^m 1000 Hz

Do sformułowania orzeczenia o dokładności sprawdzanego multimctru na danym podzakresie i w danym paśmie częstotliwości potrzebne jest wyznaczenie wartości największego błędu na tym podzakresie i w tym paśmie częstotliwości Problem powstaje, gdy dysponujemy tylko cząstkowym zbiorem wyników pomiaru (wyniki sprawdzenia dla jednego lub dwu wskazań) Problem rozwiązuje się następująco Wybiera się wynik pomiaru wykazujący błąd częstotliwościowy o największej w danym paśmie wartości, otrzymany dla wybranego do badań wskazania Oblicza się względną wartość (w stosunku do wskazania, którego dotyczy) błędu dodatkowego (częstotliwościowego) Wybiera się to wskazanie na danym podzakresie, dla którego błąd podstawowy (otrzymany przy częstotliwości 1000 Hz) jest największy co do bezwzględnej wartości ale spośród błędów o tym samym znaku co błąd dodatkowy Przelicza się względny błąd dodatkowy na błąd bezwzględny dla wskazania, które wykazywało największą wartość błędu podstawowego (wykorzystujemy proporcjonalność). Należy zloZyć (dodać¹) błąd podstawowy i wyznaczoną składową częstotliwościową dla danego wskazania Dla tak otrzymanej wartości błędu wyznaczyć granice jej niepewności Wyznaczyć największą możliwą wartość błędu (przy danych granicach niepewności) i tę porównać z dopuszczalnym błędem badanego multimctru dla danego wskazania w danym paśmie częstotliwości

Sformułować orzeczenie co do dokładności badanego multimetru, wynikające z zakresu wykonanych badań

4.    Zbadać dokładność wskazania badanego multimctru dla napięcia o przebiegu niesinusoidalnym Badanie wykonuje się dla przebiegu trójkątnego i prostokątnego (prostokątnego symetrycznego) W tym celu doprowadzić do zacisków badanego multimetru napięcie o częstotliwości 1000 Hz i kolejno o wymienionych przebiegach. Zapewnić jedno ze wskazań (możliwie duże), dla których wykonywane były badania w p 3. Wyznaczyć błędy wskazania przyrządu dla badanych przebiegów (w ocenie niepewności uwzględnić ewentualnie błędy dodatkowe multimetru wzorcowego).

Sprawdzenie (spekulacyjne) dokładności zasady pomiaru napięcia skutecznego zastosowaną w badanym multimetrze. Przyjmując, Ze kształty generowanych przebiegów probierczych oraz dokładność pomiaru napięcia skutecznego multimetrem wzorcowym są dokładne, wyznaczyć amplitudy zastosowanych napięć probierczych, a następnie ich średnie wyprostowane wartości Otrzymane średnie „przeskalować na wskazania" wartości napięcia skutecznego, tak jakby powstały z przebiegu sinusoidalnego (bo tak został wyskalowany badany multi-metr) Z takich obliczeń otrzymujemy liczbę, która jest teoretycznie oczekiwanym wskazaniem badanego multimetru dla napięcia o danym przebiegu Porównać je z faktycznym wskazaniem i wyznaczyć rozbieżność Porównać otrzymaną rozbieżność z wcześniej wyznaczonym błędem wskazania dla odpowiedniego kształtu przebiegu. Ustosunkować się do wyników

5.    Wyjaśnić, dlaczego w punktach 3 i 4 zalecono pomiary przy tym samym wskazaniu, dla którego wykonywano badania w punkcie 2.

5.8. Badanie dokładności mostka przy użyciu wzorców RLC 5.8.1. Wprowadzenie

Do wykonania tego ćwiczenia potrzebna jest wiedza zawarta w p 4 3 i 4 4

2)4

Celem ćwiczenia jest poznanie procedury badać dokładnościowych uniwersalnego mostka przy użyciu wzorców RLC Przez uniwersalny mostek rozumie się tu mostek o widu funkcjach pomiarowych i o wielu podzakreaach dla każdej funkcji Istotnym problemem w takim zadaniu jest przygotowanie odpowiedniej procedury postępowania, przy której wykonując mo2liwie małą liczbę pomiarów mamy podstawy ocenić dokładność mostka w o wiele większym zakresie (lub w pełnym zakresie) niż wynikałoby to bezpośrednio z zakresu doświadczalnych badań Opracowanie takiq procedury (planu badań) nazywa się też w miernictwie przygotowaniem strategu pomiarów Strategię tworzy się na podstawie analizy obiektu badań, czyli w naszym przypadku uniwersalnego mostka oraz celu badań, czyli w naszym przypadku - dokładności

Badany mostek ma sześć funkcji pomiarowych (w tym trzy są fiinkcjami pomiaru wielkości Rl,C). Każda funkcja pomiarowa realizowana jest na ośmiu podzakresach Wykonanie sprawdzeń dla dużej liczby wskazań na każdym podzakresie każdej funkcji wymagałoby wykonania olbrzymiej liczby pomiarów. Gdy rozpatrzy się jednak schematy układów pomiarowych (rys. 5 7) zastosowanych w przyrządzie do realizacji poszczególnych funkcji i uświadomi się sobie, z czego wynika błąd przyrządu, to można wskazać taką procedurę postępowania, przy której wystarczy wykonać ograniczoną liczbę odpowiednio zaplanowanych pomiarów, żeby uwierzytelnić dokładność przyrządu dla danych funkcji pomiarowych i danych pod zakresów, tzn potwierdzić lub zakwestionować deklarowaną przez wytwórcę charakterystykę dokładnościową

Rozpatrzymy zagadnienie dla funkcji pomiarowych RLC.

Z warunku równowagi (gdy napięcie na detektorze Ud-0) układów mostkowych przedstawionych na rys. 5 7 wyprowadza się zależności (5.4) dla rezystancji Rx, dla pojemności Cx oraz dla indukcyjności Lx W badanym przyrządzie układ mostka (rys. 5.7a) do pomiaru rezystancji zasilany jest napięciem stałym, układy mostków do pomiaru Cr i Lx (rys 5 7b i c) zasilane są napięciem przemiennym o częstotliwości 1 kHz Przy prądzie zmiennym do stwierdzenia stanu równowagi mostka detektor D działa w układzie fazoczułym (np w układzie pokazanym na rys. 3.5). Jak wiemy, oznacza to, że równocześnie detektor jest selektywny, co zapewnia równoważenie tylko ze względu na napięcie probiercze I kHz (na napięcie np harmonicznych detektor me reaguje) Fazoczułość oznacza też, że wskazanie detektora zmienia znak, gdy zmienia się „znak" mezrównoważenia. W zastosowanym układzie przyrządu wskazania detektora są proporcjonalne do „składowej biernej napięcia mezrównoważenia"

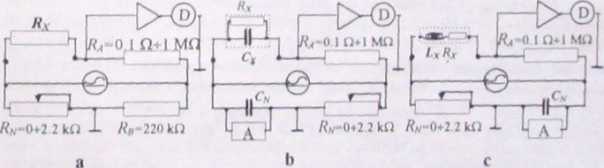
Rys. 5.7. Schematy układów mostkowych zastosowanych w badanym przyrządzie do pomiaru: a - rezystancji, b - pojemności, c - indukcyjności (zachowano oznaczenia takie jak w dokumentacji przyrządu)

Natomiast „składową czynną napięcia mezrównoważenia” zastosowano do sterowania „konduktancją A ", tak żeby przy pomiarze pojemności Cr kondensatora o konduktancji lub przy pomiarze indukcyjności cewki Lx o rezystancji Rx ręcznemu równoważeniu mostka za pomocą Rn towarzyszyło automatyczne (samoczynne) równoważenie „konduktancją A"

235