Mechanika!5

Metoda dokładna
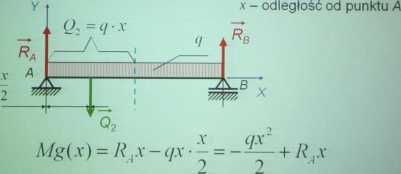
Miejsca zerowe: nY2 ( n \ ,
2.2 ii
x = 0vx= —= —2. = SLZ = /
q q q
Wyszukiwarka
Podobne podstrony:
Mechanika!6 Dla momentu gnącego:Mg(x) = -C^- + RAx Wyznaczone zostały miejsca zerowe:x=0vx=l Odcięta
Mechanika!8 Siła tnąca:T(x) = qxm = dMg(x) dx + Rax + RA — —qx + RA u Miejsca zerowe: - qx + Ra = 0
Mechanika$8 /. xe [0; 0,4) Mg(x) = -500*2 + 900* Miejsca zerowe: - 500a:2 + 900jc = O x(-500x + 900)
metoda bisekcji Newtona iteracji prostej dokładne miejsce
wartości miejsca zerowego funkcji ciągłej — metoda
Zjazd 3 str 3 16. Znaleźć miejsca zerowe funkcji. a) /(ar) = x5 — 2x4 — x + 2 d) 4
img084 84 84 n+1 rr.+ i x e < tQ,t > Funkcja g ma m+l krotne miejsce zerowe w punkcie &
o7 (2) pę. Do ustalenia dokładnego miejsca naklejenia można wykorzystać pozostałą część —
więcej podobnych podstron