Nowy 4 (7)

Jak działa FFT 225

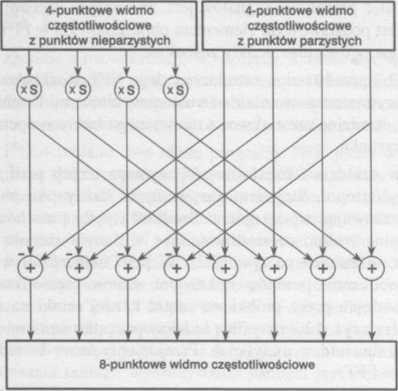
Rys. 12.5. Sieć przepływu sygnałów w syntezie FFT. Przedstawiono tu sposób łączenia ze sobą dwóch 4-punktowych widm częstotliwościowych w celu utworzenia pojedynczego, 8-punktowego widma częstotliwościowego. Operacja x S oznacza, że sygnał jest mnożony przez sinusoidę o odpowiednio wybranej częstotliwości

W celu dopasowania do siebie sumowanych widm, rozrzedzanie zerami sygnałów w dziedzinie czasu wykonuje się dwoma nieco różniącymi się sposobami. W jednym sygnale zerami są punkty nieparzyste, podczas gdy w drugim są nimi punkty parzyste. Tak więc jeden z sygnałów w dziedzinie czasu (OeOfOgOh na rys. 12.4) jest przesunięty w prawo o jedną próbkę. Takie przesunięcie w dziedzinie czasu odpowiada pomnożeniu widma przez sinusoidę. Aby to zrozumieć, przypomnijcie sobie, że przesunięcie w dziedzinie czasu jest równoważne splotowi sygnału z przesuniętą funkcją delta. Powoduje to mnożenie widma sygnału przez widmo przesuniętej funkcji delta. Widmo przesuniętej funkcji delta jest sinusoidą (patrz rys. 11.2).

Na rys. 12.5 przedstawiono sieć przepływu sygnałów, obrazującą łączenie dwóch widm 4-punktowych w pojedyncze widmo 8-punktowe. Aby jeszcze bardziej uprościć ten problem, zwróćcie uwagę na fakt, że rys. 12.5 jest utworzony przez wielokrotne powtarzanie podstawowej sieci z rys. 12.6.

Rys. 12.6. „Motylek” FFT. Jest to podstawowy element obliczeniowy w FFT, który dwa punkty zespolone przetwarza na dwa inne punkty zespolone