P1010852 (2)

332 i. LUKI

<5(i - jcsi przemieszczeniem punktu przyłożenia siły X_t po kierunku jej działania, na skutek działania siły X,m I.

<$u - jest przemieszczeniem punktu przyłożenia siły X, po kierunku jej działania, na skutek działania siły = 1,

h, - jest przemieszczeniem punktu przyłożenia siły X, po kierunku jej działania, na skutek działania obciążenia zewnętrznego.

Zgodnie z twierdzeniem Mazwella

6_U<=5_U,

M_it N_t, Tj - są odpowiednio momentem zginającym, siłą podłużną i poprzeczną w układzie zastępczym od X_i-l) M„, A'_p, T_p - są odpowiednio momentem zginąjącym, siłą podłużną i poprzeczną w układzie zastępczym od obciążenia siłami zewnętrznymi; 9 -współczynnik zależny od kształtu przekroju poprzecznego.

W przypadku pominięcia wpływu sił podłużnych i poprzecznych na wielkości przemieszczeń wzory (7.3) przyjmą postać

iBI ff*t% 11113 i

0 0 0

Natomiast gdy układ jest jednokrotnie statycznie niewyznaczalny, równanie kanoniczne metody sił przyjmie postać

(7.5)

stąd

r' ej

hi

(7-6)

IS

Dla układu dwukrotnie statycznie niewyznaczalnego równanie kanoniczne metody sił przedstawia się następująco:

2flój|+XjÓ|₂+ól, = 0,

X,ó_łl+^₂ó_2ł+ó₂,=0.

Przy n-kr ornie statycznie niewyznaczalnym układzie będziemy mieli n równań kanonicznych metody »Ł

7.2.1. Zmienność momentów bezwładności przekroju luku

Najczęściej przy łukach zmienność momentu bezwładności (rys. 7.10) przyjmiąe się według wzoru

J,-J_t - moment bezwładności w przekroju odległym o z od wezgłowia, J_c — moment bezwładności w zworniku, f - kąt nachylenia stycznej do osi łuku względem poziomej osi układu.

W lukach statycznie niewyznaczałnych, w przypadku pominięcia wpływu sił podłużnych i poprzecznych na wielkości nadliczbowe, przemieszczenie, jak wyprowadzono w p. 7.2, wyraża się wzorem

J

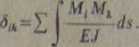
0

Z powyższego wzoru wynika, że aby otrzymać odpowiednie przemieszczenie należy całkować po luku. Jeżeli więc przyjmujemy w łuku parabolicznym zmienność momentów bezwładności, wyrażoną wzorem (7.8) oraz gdy podstawimy do wzoru na S_ik za d_M= =<£t/cosę>, to otrzymamy

*

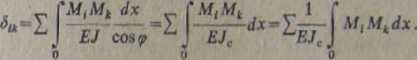
(7.9)

Stąd wynika, że wartość można obliczyć w luku parabolicznym drugiego stopnia, przy założeniu J—jJcosę>, całkując po rzucie łuku, zamiast po łuku (rys. 7.11). Sposób ten stwarza możliwości korzystania z całek graficznych jak przy prętach prostych.

Gdy kształt osi łuku lub zmienność momentów bezwładności nieznacznie odbiega od powyższych założeń, można obliczenie takie przeprowadzić z uproszczeniem, ponieważ różnice w stosunku do obliczenia dokładnego będą niewielkie.

y

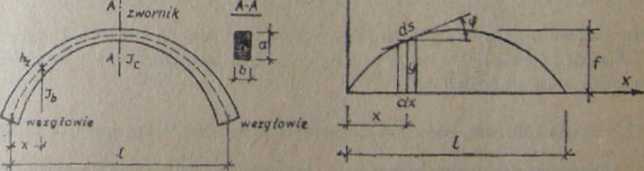
Rys. 7.10. Zmienność przekroju na długości łuku Rys. 7.11. Sprowadzenie osi tuku do rzutu pozio-

mego

Powyższy przebieg zmiany momentu bezwładności jest wystarczająco dokładny również i dla łuków o stałym przekroju, przy wyniosłościach luków £<0,20. W łuku o stałym przekroju JJJ_X<*1, a zatem ze wzoru JJJ_x»cmę_x, cosęy=l.

Ponieważ takie założenie jest niezgodne z rzeczywistością, przyjmuje się często drugie