P3200284

148

148

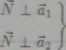
=> fi II G| X S₂ =    4

1-2

3    *]

-3 1 j = -15 -i- 10 j + 30-fc = 9    2

= [—1-5, -10,30] = —5 - [3,2, -6]

Skoro N = [3,2, —6] i płaszczyzna o przechodzi przez punkt P_x(9, -2.0). to o: 3(* — 9) + 2(y + 2) — 6z = 0 3x + 2y — 6z — 23 = 0.

.    |3-0 + 2-(—7) - 6-2 - 231 I- 14-12-23)

^i{P,'^a)--. v/9+4+36--^---

— 49|    49

7    7

Odp.ł Odległość między prostymi /j, ł₂ wynosi 7.

G8. Znaleźć najbliżej siebie położone punkty Qi, Qj odpowiednio na prostych /j, /₂ z zadania G7.3).

Punkty Qi, Qz będą leżały najbliżej siebie, gdy wektor Q\Qi będzie prostopadły do obu prostych. W przypadku prostych skośnych istnieje tylko jedna para takich punktów.

(Długość wektora Q\Qi jest równa odległości między prostymi /j. />. zatem w ten sposób też można obliczyć odległość między prostymi skośnymi.)

QiQi 3. &i — [4, —3,1] A    02 =[-2,9,2]

Punkt Qi leży na prostej li, natomiast punkt Qi leży na prostej h- Obie proste zapiszemy równaniami parametrycznymi.

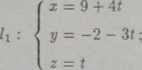
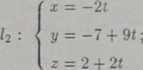
Q\Q% —. [—2to — 9 — 4tj, —7 + 9*₂ + 2 + 3*i, 2 + 2*₂ — ti] = = [-4*i - 2*2 - 9, 3*i + 9*2 - 5, -*i + 2*2 + 2]

Zauważyliśmy wcześniej, że ty\Qi jl «i A Q\Ot i- *i, ^w*?^c wchodzi QiQz o«i = 0 A QiQj oa₂ =0.

-16*i-8t₂-36-9*i“27*2+15-ti+2<j+2 = 0

8lj +41, + 18+27li +81*j -45-2*i +4*2 +4*0

-26*i - 33*2 - 19 « 0 33*i + 89*2 - 23 = 0

26*, + 33*a    -19

33*i +89*2 = 23

26 33 33 89 -19 33 23 89 26 -19 33    23

W = W_l = w₂ =

= 26 • 89 - (33)* = 2314 - 1089 = 1225 = 25 -49 * -19 • 89 - 23 * 33 * -1691 - 759 * -2450 * -50 • 49 = 26 • 23 + 33 • 19 = 598 + 627 = 1225

W_x -50 • 49 ^<ł " W ~ 25-49 “

Zatem otrzymujemy

Qi (9 + 4 • (-2), -2 - 3 • (-2), -2), czyli Q, (1,4, -2);

Qa (-2-1, -7 + 9-1, 2 + 2-1), etyli Q_a(-2,2,4).

Odp.: Najbliżej siebie są położone punkty Qi(l,4, -2), Q,(—2,2,4).

Jeżeli chdelibyimy teraz obliczyć odległość między prostymi l\, lj, to d(łi,l₂) = |q7Q2| = v/(~3)⁴ + (-2)^J + 6² = V9 + 4 + 36 = >/49 = 7.

G9. Wyznaczyć równanie płaszczyzny, w której leżą proste z zadania G7.2).

Z równań prostych danych w zadaniu G7.2) odczytujemy: dla prostej l_x jest Pi (—2,6, 7), o, = (4, —6, —8J, natomiast dla prostej /, jest Ą (7,2,0), a, = [—6,9,12). Zbadaliśmy, że proste są równoległe, ale nie pokrywają się.

P\Pi = [9, -4, -7]