P4250067

w turbinie ekspandują gezy spaliaowe. Wiążą się z tym trudności w p₀_ glądowym przedstawieniu obiegu otwartego w wykresie en tropowym (T—s lub

/-sj.

1.1. Obieg idealny Joułe’a-Braytona

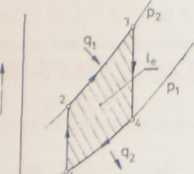
Pomijając komplikacje związane ze zmianą rodzaju czynnika w obiegu oraz nie uwzględniając zależności wynikających z chłodzenia turbiny przyjmiemy układ wyidealizowany, w którym pracuje czyste powietrze. Założymy, że czynnik ten możemy traktować jako gaz idealny w rozumieniu Ochęduszki [9], tj. przyjmiemy ciepło właściwe gazu c, = const oraz wykładnik izentropy x — cjc„ = const, taki sam dla przemiany w kompresorze i w turbinie. Rozważać będziemy obieg idealny z izentropową kompresją, izentropową ekspansją i izobarycznym doprowadzeniem ciepła do obiegu. Ponadto przyjmujemy, że strumień gazu pracującego w kompresorze i turbinie jest taki sam, m_k m m_T. Opisany proces odpowiada obiegowi teoretycznemu Joule’a-Brayto-na. przedstawionemu na rysunku III.2.

T

s

Rys. Hf.2. Idealny obieg porównawczy Joulc’a 'Jraytona

Sprawność takiego obiegu

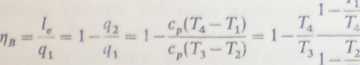
Wprowadzając stosunek ciśnień

P i Pa

otrzymamy z równania izcntropy

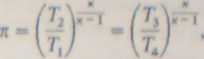
stąd

albo

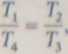
i-w

H

m    h

T,    T_t

co uwzględnione we wzorze (III.l) daje

»/«

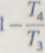
1 — n

Ze wzoru (III.2) wynika interesujący wniosek, że sprawność obiegu Jou-lca-Hraytona rj_B zależy tylko od stosunku ciśnień p_i/p_l i rodzaju gazu, tj. od wykładnika x,

Wykres rj_B - q_B(n) przedstawiono na rysunku III.3.

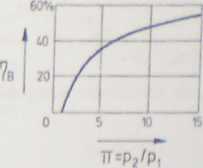
Rys. III.3. Sprawność obiegu idealnego Joule’a-Braytona, x ■ 1,4

Temperatura górna obiegu T₃ nie ma wpływu na sprawność ij,,, natorrńo. ze wzrostem T₃ rośnie praca jednostkowa obiegu, reprezentowana pulem powierzchni 1—2—3—4—1 na rysunku III.2,

K^m Wb^i*

gdzie /_r, l_k — praca odpowiednio turbiny i kompresora.

Zc wzrostem pracy /, maleje strumień gazu potrzebny do realizacji zadanej mocy efektywnej

N. N_e

m = •— --——.

0 ^rla^cf(Ti ~ ^2)

Wymiary silnika i jego koszt rosną, gdy rośnie strumień czynnika pracują cego. Tak więc z tego punktu widzenia wartość temperatury górnej T₃ nie jest obojętna.

Przebieg sprawności obiegu rzeczywistego w funkcji stosunku ciśnie;i