P3200159

246 4. Analiza skupie,

Liczebności n. oraz n, nazywamy liczebność iami brzegowymi.

Podstawą do konstruowania miar podobieństwa (współzależności) dwóch cech nominalnych jest kryterium niezależności, które w odniesieniu do klasyfikacji wielodzielczej (politomicznej) jest następujące: jeżeli cechy A i B są całkowicie niezależne w całej zbiorowości, to dla wszystkich klas A_t B zachodzi równość

n_J% * ⁿ*₍

_n - (i= 1,2,... ,r;j = 1,2,... s)    (4.54)

n

Oznaczmy dla wygody teoretyczne liczebności w komórkach tablicy wielodzielczej przez n_;i (prawa strona równości 4.54). Jeżeli cechy A i B nie są całkowicie niezależne, to wielkości i n. będą różne dla różnych par kategorii (i, j), czyli klas klasyfikacyjnych A, B_l. Różnicę między zaobserwowaną liczebnością w komórce tablicy wielodzielczej a liczebnością oczekiwaną przy założeniu, że dwie cechy są niezależne w sensie probabilistycznym

<5* = n.. - n..    (4.55)

nazywamy kontyngencyjnością lub wielodzielczością (zob. Kendall i Buckland, 1975), przy czym

2A =0 (i= l,2,...,r) oraz Ź<5,=0 (j=l,2,...,s)    (4.56)

1*1 ⁹    i—l ⁹

Łącznym miernikiem skojarzenia dla wszystkich A, jest wyrażenie

i

= n

'=i ;-i n_imn .

(4.57)

zwane kontyngencyjnością kwadratową, znane powszechnie jako statystyka chi-kwadrat. Jest to wielkość niezależna od znaku różnic <5. i przyjmuje wartości X¹ > Ol przy czym jeżeli cechy są niezależne (ó.. = 0), to x² — 0. Ponieważ nie jest określona góma granica tej statystyki, to nie może ona być odpowiednia jako miara współzależności i podobieństwa.

Częściowo tę niedogodność usuwa miernik skojarzenia

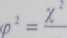
n

który nosi nazwę średniej kontyngencyjności kwadratowej (ang. mean scjuarecon-tingency). O ile jednak dla tablicy o wymiarach 2Xs (s> 2) 0 < (p¹ < 1 i może występować w roli współczynnika, to dla tablicy r X s <p² > 0, a jego wielkość zależy od wymiarów tablicy.

pearson zaproponował inną miarę, która umożliwiałaby bardziej jednoznuc/.

współzależności cech. Takim współczynnikiem jest

\ 1+ \ⁿ+X

(4.59)

znany p°d nazwą współczynnika przypadkowości (lub koniyngencji) Pctnona iang coefficient ojcontingency). Jeżeli ą wzrasta toC rośnie do wartości jeden, lecz nigdy jej nie osiąga. W tablicy kwadratowe) r X r górną granicą dlaC jest

(4.60

(np. w tablicy 2x2 mamy C = V1/ 2 = 0,707). Nieznana jest górna granica dla la blicr X s (r^ s). Dwa współczynnikiC nie są porównywalne chyba że pochodzą z tablic o tych samych wymiarach.

Inna próba unormowania miary *p² pochodzi od Czuprowa Czynnikiem nor muiąeym jest tu średnia geometryczna dwóch wielkość i r — \ oraz s — 1 czyli -1) (j — 1). Doprowadziło to do miernika znanego szeroko jako współczynnik

TCzuprowa o postaci

(4.61)

Uwzględniając wzory (4 58) i (4 59). możemy go tez zapisać vako

(4.62)

\ (1- C² )4ir — l)(s -1)    \ riyj{r — lKs-U

Dla tablic o wymiarach r\r przyjmuje on w artosci 0 < T < 1 zas dla tablic rx$(r*s) 0<T<1

Nieco zmodyfikowaną w stosunku do współczynnika Czuprowa iesi propozycja Cramera, który maksymalizował <p‘ w sposob następujący

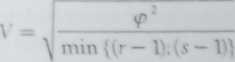
(4.63)

Wyjaśnienie istoty wyrażenia min {(r — IV (s — \)J jest następujące. W tablicy kwadratowej idealna zależność występuje, gdy n.. = n.₍ = n dla wszystkich i. Oznacza to. że wszystkie kategorie, poza r klasami na przekątnej, są puste. Jeżeli wę wzorze na chi-kwadrat (druga postać wzoru 4.57) uwzględnimy relację — n„. to wartość statystyki chi-kwadrat wyniesie n(r — 1) i jest to maksymalna wartość <p ’ Jeśli teraz rozważymy tablicę prostokątną(r* $), to idealna