P3200168

264 4. Analiza skupień

• Wyszukujemy w macierzy najmniejszą odległość między dwoma obiektami. Jest to odległość między obiektami 2 i 7, która wynosi

min{d_a } = d_ł7 =2,17

co oznacza, że pierwsze skupienie p utworzą obiekty {2;7}. Skupienie to reprezentowane będzie od tej pory (w kolejnej macierzy odległości) przez kolumnę i wiersz o numerze 2.

• Redukujemy macierz D¹⁰'. usuwając siódmy wiersz oraz siódmą kolumnę, i przyjmując za odległość d, nowego skupienia od pozostałych obiektów mniejszą z dwóch odległości d_{2 l} i d₇. (i = 1,3,4,5,6), np. d_x (2 7) = min{ 2,75:4,23} = 2,75, lub przeliczając odległości według wzoru (4.96), np.

d_lr 4,23 +^2,75-^4,23-2,75|= 2,75

d_2p = - • 8,54 + ^ • 4,91 - ^|8,54 - 4,91] = 4,91 itd.

W wyniku pierwszego kroku grupowania otrzymujemy zatem następującą macierz odległości

I 1	2,75	3,50	7,64	5,11	4,05
2,75	0	4,91	5,19	6,78	3,18
3,50	4,91	0	6,20	7,58	9,23
7,64	5,19	6,20	0	4,17	4,22
5,11	678	7,58	4,17	0	2,51
4,05	3,18	9,23	4,22	2,51	0_

• Czynność powtarzamy, tj. szukamy ponownie najmniejszą odległości, którą jest d₅ 6 = 2,51, i łączymy obiekty o numerach 5 i 6 w drugie skupienie. Przekształcamy ponownie odległości, w wyniku czego uzyskujemy nową macierz odległości:

0	275	3,50	7,64	4,05
2,75	0	4,91	5,19	3,18
3,50	4,91	0	6,20	7,58
7,64	5,19	6,20	0	4,17
4,05	3,18	7,58	4,17	0

• W trzecim kroku najmniejszą odległością okazuje się d, _{(2 7}, = 2,75, co oznacza, że do skupienia (2,7) dołączony zostaje obiekt o numerze 1. Opuszczamy wiersz 1 i kolumnę 1, a przeliczone odległości zbieramy w macierzy D¹".

o 3,50 5.19 3,18' 3,50    0    6.20    7.58

ir =

5,19 6,20    0    4,17

3,18 7,58 4,17    0

• Wykonujemy kolejne iteracje w taki sam sposób, dołączając tym razem do skupień już istniejących nowe elementy oraz łącząc je a podstawą tych połączeń były każdorazowo przeliczane odległości;

D ⁴¹

0 3,50 4,17 3,50    0    6,20

4,17 6,20    0

D =

0 4,17] 4,17    0

• Efekt aglomeracyjnego grupowania hierarchicznego przedstawia dendro gram, ujawniając zarówno kolejność, w jakiej tworzone były skupienia jak i po ziomy, na jakich kolejne połączenia następowały

Poziomy

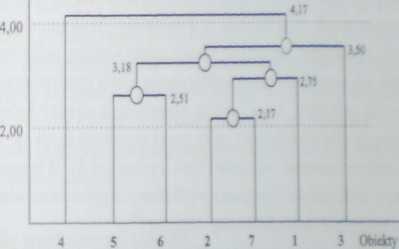
Rysunek 4.5. Dcndrogram (metoda najbliższego sąsiada)

Zauważmy, że obiekt 4. który dołączył do skupienia jako ostatni (etap 6i, ma odległość od tego skupienia 4,17, a więc najniższą z odległości tego obiektu od ja kiegokolwiek obiektu tworzącego skupienie (2.7,1,5,63) i jest to najmniejsza liczba w wierszu (lub kolumnie) 4 macierzy D ^# Podobnie obiekt 3. który na przedostatnim etapie został włączony do skupienia, ma najmniejszą /. możliwych wyjściowych odległości 3,50 (wiersz lub kolumna 3). I tak kolejno. Weźmy jeszcze czwarty etap, na którym na poziomie 3.18 połączyły się skupienia (5,6) oraz (2.7,1). Najniższą spośród odległości w dwóch podmacierzach macierzy D° ¹

1

Okazany w tym przykładzie sposób sporządzania dendrogramu jest typowy (także dla progra ^mo"’ komputerowych), niemniej istnieją i inne możliwości przedstawiania drzewka połączeń, zależ °d inwencji badacza oraz. potrzeby uwypuklenia pewnych cech połączeń (zob. Gordon, 1999)