S6303030
430 HYDRAULIKA TECHNICZNA. PRZYKŁADY OBLICZEŃ
jak np. dla koryta o żwirowym dnie i ściankach z kamienia albo koryta ziemnego bez roślinności.
Na podstawie przyjętych zależności określono skalę podobieństwa dla współczynnika szorstkości bez uwzględnienia skażenia modelu:
(16)
Ponieważ a„ =—7 = et'/6, więc współczynnik szorstkości w korycie modelowym n
m -
(17)
zaprojektowanym w skali nieskażonej miałby wartość: n = «'a"6 = 0,021 m~ms ■(—
Współczynnik ten charakteryzuje koryta z umocnieniami betonowymi.
Po wprowadzeniu skali skażonej skala podobieństwa dla współczynnika szorstkości ulegnie zmianie:
(Dcll)2/3 Dl,:
2/3 „,1/6 ■i
= D a
(18)
_| n |_
wykonanego w skali skażonej miałaby wartość:
__Jl/6 I
i
n = n'D2,3a1/6 = 0,027 m ‘"s • 1
(19)
Wśród tradycyjnych materiałów stosowanych do umocnień koryt nie ma tworzywa o takim współczynniku szorstkości, dlatego do uzyskania szorstkości koryta modelowego należy zastosować np. wióry drewniane przyklejone do podłoża.
PRZYKŁAD 15.3.
Budowla piętrząca ma przelew o wysokości p' = 19 m i szerokości Bł - 20 m. Przy przepływie miarodajnym Q' = 80,47m3/s zwierciadło wody nad koroną przelewu wznosi się na wysokość H' = l,5m. Zaprojektować model przelewu w skali 1:25. Sprawdzić jaka będzie pierwsza i druga głębokość sprzężona oraz obliczyć wysokość straconej energii przy przejściu wody przez odskok na modelu i w naturze. Obliczyć parcie dynamiczne strumienia na model przelewu oraz na przelew w warunkach naturalnych.
Parametry hydrauliczne i geometryczne modelu obliczono według kiyterium Froude’a, zgodnie z którym za dominującą w zjawisku uznaje się siłę ciężkości.
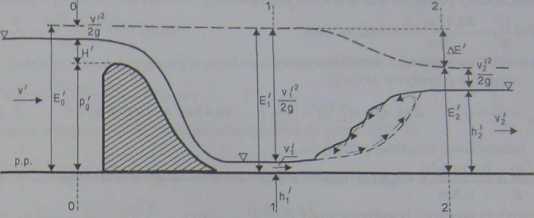
RYSUNEK 15.2. Schemat budowli piętrzącej w warunkach naturalnych

/
wzniesienie zwierciadła wody nad koroną przelewu H:
H_
9
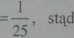

1,5 m
-= 0,06 m
25
f wysokość przelewu pK:
\P'_ !■
p, : 25' " r * 25 25
✓ szerokość przelewu B:
W warunkach naturalnych przez przelew przepływa woda o natężeniu Q'=80,47 m3/s i średniej prędkości:
kr S? 80,47 m3/s A ,
V =tó+«')a' = (T9mVl,5m).20m Wm/S I
Stąd p. =—
B 1
—=—, stąd B 25

Pg 19 m
= 0,76 m
Wyszukiwarka
Podobne podstrony:
S6303022 416 HYDRAULIKA TECHNICZNA. PRZYKŁADY OBLICZEŃ natury niż wymiary samego modelu. Jeszcze bar
83176 S6303027 424 hydraulika techniczna, przykłady obliczeń Dla pierwszego przypadku powinno się st
więcej podobnych podstron