Scan Pic0085

duje trzykrotny wzrost energii kinetycznej fotoelektronu. Praca wyjścia elektronów z tego metalu jest równa:

C. W--E D. W = —E 2    3

A. W=2E B. W=E

Zadanie 6.6

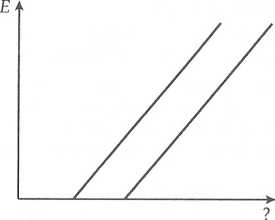
Wykresy przdstawiają zależność

maksymalnej energii kinetycznej

E_k fotoelektronów od:

A.    natężenia światła dla dwóch metali

B.    częstotliwości światła dla dwóch metali

C.    częstotliwości światła przy dwóch jego natężeniach

D.    natężenia światła przy dwóch jego częstotliwościach

Zadanie 6.7

U

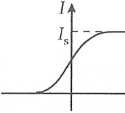
Rysunek pokazuje zależność natężenia prądu płynącego przez fotokomórkę od napięcia przy ustalonym oświetleniu fotokomórki. Przekroczenie wartości prądu nasycenia wskazanej na wykresie można osiągnąć przez

A.    przesłonięcie źródła światła filtrem fioletowym

B.    zwiększenie napięcia przyłożonego do fotokomórki

C.    zmniejszenie odległości między fotokatodą i fotoanodą

D.    wstawienie między źródło światła a fotokomórkę soczewki skupiającej światło na fotokomórce

Zadanie 6.8

Lampa rentgenowska emituje fotony o maksymalnej częstotliwości równej 9,5-10¹⁸ Hz. Jeżeli przyjąć, że stosunek stałej Plancka do ładunku elektronu

— = 4-10"¹⁵ Vs, e

to napięcie przyspieszające w tej lampie jest równe około:

A. 3-10³ V B. 38-10³ V C. 38-10⁴ V D. 30-10⁵ V

Zadanie 6.9

Znając szybkość światła c, ładunek elementarny e oraz minimalną długość fali A_min promieniowania rentgenowskiego wysyłanego przez lampę zasilaną napięciem U, można wyliczyć stałą Plancka korzystając z zależności:

Zadanie 6.10

Stosunek energii fotonu promieniowania rentgenowskiego o długości fali 10^-10 m do energii fotonu światła fioletowego o długości fali 4-10"⁷ m jest równy:

A. 4-10^-17

B. 2,5-10'⁴    C. 2,5-10^-2    D. 4-10"³

Zadanie 6.11

B. 10"³ kgm-s^-1 D. 3-10'¹¹ kgm-s"¹

Foton o energii 9-10"¹⁹ J ma pęd równy A. 3-10'²⁷ kgm-s'¹    B.

C. 10“³⁵ kgm-s"¹    D.

Zadanie 6.12

Jeżeli anodę lampy rentgenowskiej bombardują elektrony o pędzie p, masie m i ładunku q, to maksymalny pęd kwantów emitowanego przez nią promieniowania jest równy:

2 mc

p²

B. JS+

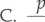
mc

2

mc

2

D. p

Zadanie 6.13

Jeżeli do elektrod lampy rentgenowskiej przyłożono napięcie U, to pęd fotonu odpowiadającego krótkofalowej granicy widma jest równy:

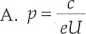
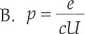
C. p = -U    D.p =

e

eU

c

- 169 -