skan0020 (5)

Stany skupienia materii 23

T= 273,15 + 23,5 = 296,65 K, R = 8,314 J • mor¹ • KT¹.

Zatem

= 1,653 -10-⁴ kg (0,1653 g). ■

22,99 -10~³ • 745 • 1,01325 • 10⁵ • 178,5 • 10~⁶ 760 • 8,314 • (273,15 + 23,5)

Ciśnienie mieszaniny gazów p jest sumą ciśnień parcjalnych składników (prawo Daltona)

P = Y.Pn    (2-10)

gdzie pj = Xjp, Xj zaś jest ułamkiem molowym składnika i w mieszaninie

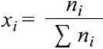
Przykład 2.2. W pewnej temperaturze, pod ciśnieniem 1 bara zmieszano po 1 dm³ H₂, N₂ i Ar. Obliczyć ciśnienia parcjalne gazów' w' mieszaninie.

Rozwiązanie. Zgodnie z hipotezą Avogadra dla T= const ip = const

~ ^ł7H₂>    *N₂ ~ «N₂ ^oraz ^Ar ~ ⁿAx-

Ułamki molowe poszczególnych gazów wynoszą

__ⁿu₂_ _ ____L

^Xli2 ~    «H₂ + «N₂ + nAr ^_ Vh₂ + ^N₂ + ^Ar    3 ’

•^vH₂ ⁼ *N₂ ⁼ xAt ⁼ J >

a z prawa Daltona wynika, że

Ph₂ ⁼ Pn₂ ⁼ Pat ~ T ' 1 ~ T hara. ■

Oprócz izotermy (2.2), izobary (2.4) i izochory (2.6) definiuje się też adia-batę gazu idealnego. Odwracalną przemianę adiabatyczną takiego gazu opisuje

w'zór
gdzie:	pV^K - const,	(2.11)
	k = Cp!Cv	(2.12)
oraz	ypCy/R = conS|}	(2.13)
	T^cP^/R/p = const.	(2.14)