skan0038 (4)

Stany skupienia materii 41

Przykład 2.12. Obliczyć stałą Eótvósa oraz temperaturę krytyczną cykloheksanu na podstawie poniższych danych⁽⁶h

T[ K]	283	293	303	313	323
o [mN • m^_1]	26,15	24,95	23,75	22,45	21,35
d [g • cm"^3]	0,7879	0,7786	0,7691	0,7596	0,7499

Rozwiązanie. Najlepiej skorzystać w tym celu z równania Eótvósa ( 2.47). Molową energię powierzchniową cieczy oblicza się z równania (2.46), np. w 283 K (wszystkie wielkości w SI)

0 = o

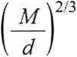
= 26,15 • 1(T³ •

/ 84,162 • 1Q~³ \^{2 3} l 0.7879 • 10³ /

= 58,87 • 10~¹[J • mor²'³].

Wyniki obliczeń molowej energii powierzchniowej cykloheksanu zestawiono w tab. 2.4.

Tabela 2.4

T[ K]	0 • 10^1 [J • mol^-273]
283	58,87
293	56,62
303	54,34
313	51,79
323	49,68

Zapisując wyrażenie (2.49) w postaci

0 = k(T_c-6)-kT=a + bT,

znajdujemy z parametrów równania linii prostej k = -b • 10 ¹ = 2,32 -10 ² .1 • mol ²'³-•K"¹; T = 6 - alb = 542,6 K.

1

K.P. Miszczenko, A.A. Rawdiel. Zbiór wielkości fizykochemicznych, PWN, Warszawa

2

1974, s. 108-113.