skanuj0104

-    okręgi kół nie ulegną zniekształceniu, a powierzchnie czołowe pozostaną nadal płaskie,

—    promienie narysowane na powierzchniach czołowych pozostaną po odkształceniu nadal liniami prostymi,

—    tworzące odchylą się od pierwotnego swego położenia o pew-ien kąt y, zwany kątem odkształcenia postaciowego,

-    powierzchnie czołowe pręta obrócą się względem siebie o pewien kąt (p, zwany kątem skręcenia.

Na podstawie tych spostrzeżeń można wnioskować, że 'wszystkie przekroje poprzeczne prętów o przekroju kołowym pozostają w trakcie skręcania płaskie, a promienie tych przekrojów pozostają liniami prostymi. Jeżeli z pręta skręcanego momentem M_s wytniemy (dwiema płaszczyznami prostopadłymi do osi pręta) walec o wysokości dx (patrz rys. 8.2b), to wartość kąta odkształcenia postaciowego na powierzchni zewnętrznej jest równa

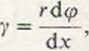
(8.1)

a na powierzchni określonej dowolnym promieniem p

(8.2)

_ pd<p

'^,p djc ‘

Ponieważ stan odkształcenia elementu wyciętego z pręta poddanego skręceniu jest identyczny z przypadkiem czystego ścinania, można wykorzystać zależność wynikającą z prawa Hookea dla ścinania:

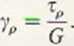
(8.3)

Łącząc zależności (8.2) i (8.3) otrzymujemy

r„ = Gp^.    (8.4)

Z warunków równowagi pręta skręcanego (patrz rys. 8.2c) otrzymujemy związek

Af, = Jv>dF.    (8.5)

Po podstawieniu zależności (8.4) do wzoru (8.5) otrzymujemy: a) W7:ór na kąt skręcenia odcinka pręta kołowego o wysokości dx i promieniu r:

127