skanuj irfanview extract03

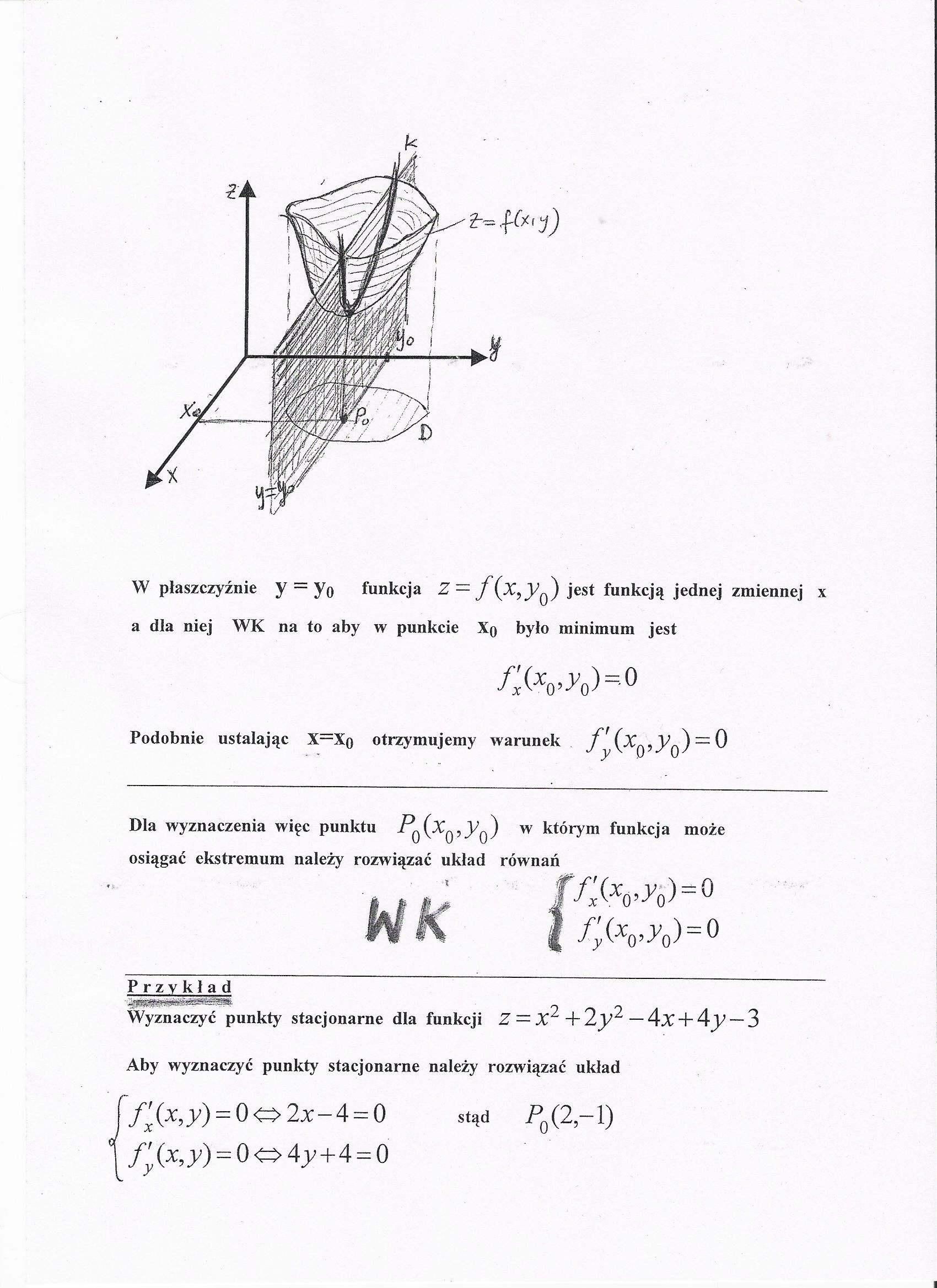
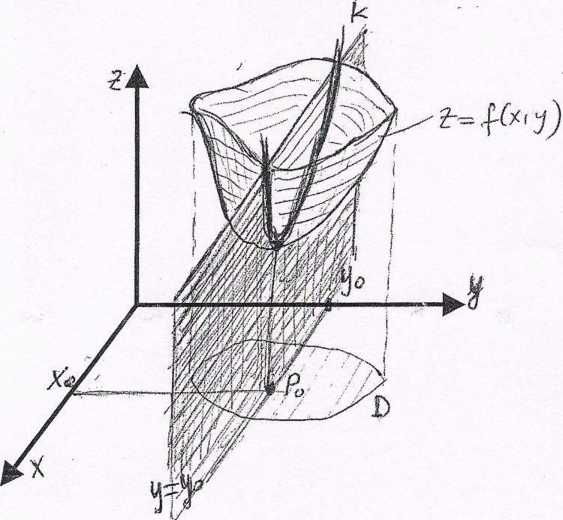
W płaszczyźnie y — yo funkcja Z — j {x,yjest funkcją jednej zmiennej x a dla niej WK na to aby w punkcie Xq było minimum jest

/*(W. o)=-°

Podobnie ustalając X=Xq otrzymujemy warunek    ,y^) — 0

Dla wyznaczenia więc punktu P^ (Xq , y^) w którym funkcja może osiągać ekstremum należy rozwiązać układ równań

J/;(vo)=⁰

1%|    O^o) ^{= 0}

Przykład

Wyznaczyć punkty stacjonarne dla funkcji z = x² + 2y² - 4x+4y - 3 Aby wyznaczyć punkty stacjonarne należy rozwiązać układ

f'_x(,^x,y) = Q<=> 2x-4 = 0 stąd i^?0(2,-l)

f'_y(x,y) = Q<^>Ąy+A^0