skanuj irfanview extract02

Oczywiście powyższe warunki (w oparciu o które wyznaczamy punkty stacjonarne ) są tylko warunkami koniecznymi ale nie wystarczającymi. Przykład

.    .' v/.    ..    • rr*

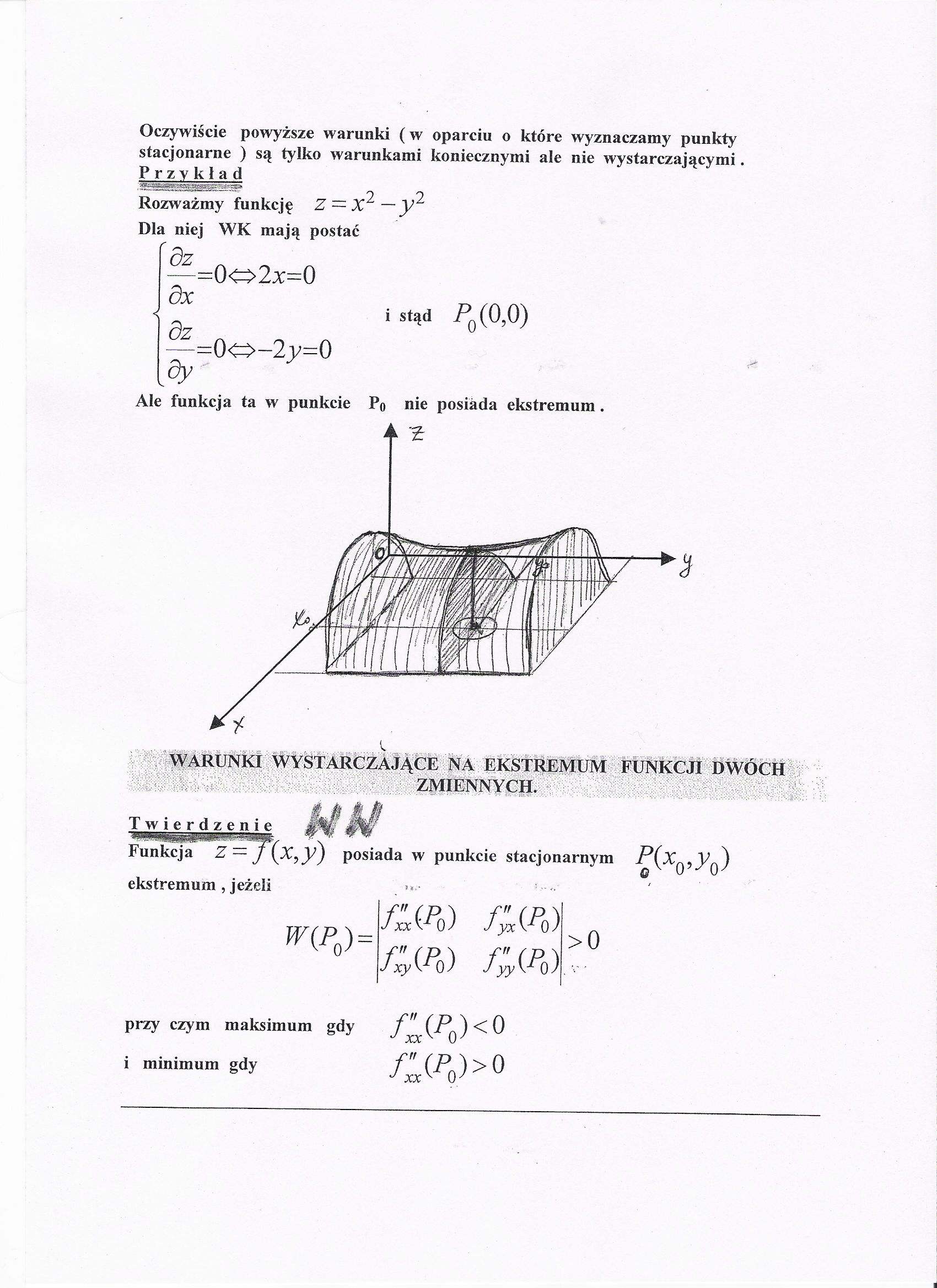
Rozważmy funkcję Z = X^

Dla niej WK mają postać

f)z

—=0<=>2x=0

i stąd P_Q (0,0)

dx

0<=>-2y=0

dz

dy

Ale funkcja ta w punkcie Po nie posiada ekstremum .

WARUNKI WYSTARCZAJĄCE NA EKSTREMUM FUNKCJI DWÓCH

ZMIENNYCH.

ekstremum , jeżeli

Twierdzenie Funkcja Z — Jy

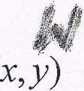
posiada w punkcie stacjonarnym

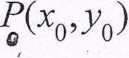
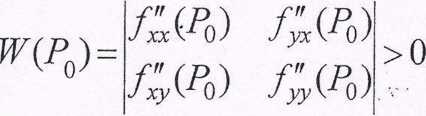
rjp₀xo

rjpj>o

przy czym maksimum gdy i minimum gdy