skrypt012

14

P{X = k} =

(n'

p^kqdiak = 0,1,2.....n (0 < p < I, q = I - p) (1.11)

Ro/kład Poissona - rozkład prawdopodobieństwa zmiennej losowej skokowej X o funkcji prawdopodobieństwa określonej wzorem

A.^ke^->'

p;X = k} = ——    diak = 0,1,2.....n (X>0)    (1.12)

k!

Rozkład jednostajny (rozkład równomierny) - rozkład prawdopodobieństwa zmiennej losowej ciągłej X o funkcji prawdopodobieństwa określonej wzorem

I

f(x) =

b - a 0

dla a < x < b

dla x < a oraz x > b.

(1.13)

Rozkład normalny - najważniejszy w statystyce rozkład zmiennej losowej X o gęstości prawdopodobieństwa określonej w zorem

j    {*-»»)'

t(x) = —j= c    ^2<r dla ⁰⁰ < x < t*°o (a>0) (i i4)

av2rc

Często rozkład normalny oznacza się symbolem N(m.a), gdzie m jest wartością oczekiwaną (średnią), a o odchyleniem standardowym w tym rozkładzie, tj. m = E(x), a = D“(X).

Rozkład normalny standaryzowany - rozkład normalny N(O.I). tzn. o funkcji gęstości określonej wzorem

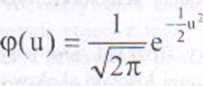
(1.15)

Wykresem funkcji gęstości jest lzw. krzywa Gaussa. Zmienna losowa U mająca rozkład N(0.1) nosi nazwę standaryzowanej lub unormowanej zmiennej normalnej.

Standaryzacja rozkładu normalnego - zmiana rozkładu normalnego N(m.o) na ro/kład normalny standaryzowany TM(O.l). Odbywa się poprzez odjęcie średniej m i podzielenie przez odchylenie standardowe a, tzn. jeżeli X ma rozkład N i m„G). to: U = (x - m) / a ma rozkład N(0.1).