41145 skrypt014 (2)

14

P{X = k} =

p^kq^n_k

dla k = O, 1,2.....n

(O < p < 1, q = I - p) Cl.li)

Rozkład Poissona - rozkład prawdopodobieństwa zmiennej losowej skokowej X o funkcji prawdopodobieństwa określonej wzorem

P|X = k) = —jTp    dla k = 0. 1.2 n (X>0)    (1.12)

Rozkład jednostajny (rozkład równomierny) - rozkład prawdopodobieństwa zmiennej losowej ciągłej X o funkcji prawdopodobieństwa określonej wzorem

1

f(x) =

b - a 0

dla a < x < b

dla x < a oraz x > b.

(1.13)

Rozkład normalny - najważniejszy w statystyce rozkład zmiennej losowej X o gęstości prawdopodobieństwa określonej wzorem

dla ~°° < x < +°°    (G>0)    (1.14)

Często rozkład normalny oznacza się symbolem N(m,<7)> gdzie m jest wartością oczekiwaną (średnią), a o odchyleniem standardowym w tym rozkładzie, tj. m = E(x), a’= D'(X).

Rozkład normalny standaryzowany - rozkład normalny N(O.ł), tzn. o funkcji gęstości określonej wzorem

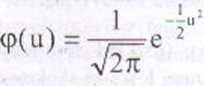
(1.15)

Wykresem funkcji gęstości jest tzw. krzywa Gaussa. Zmienna losowa U mająca rozkład N(0, l) nosi nazwę standaryzowanej lub unormowanej zmiennej normalnej.

Standaryzacja rozkładu normalnego - zmiana rozkładu normalnego N(m,<7) na rozkład normalny standaryzowany N((). I). Odbywa się poprzez odjęcie śred niej m i podzielenie przez odchylenie standardowe g. tzn. jeżeli X ma rozkład N(m.o). to: IJ = (x - m) / a ma rozkład N(0,l).